Question

【题目】已知如图，四边形中，于点，．点为边上一点，以为边作平行四边形，则最小值是__________．

Answer 1

【答案】4

【解析】

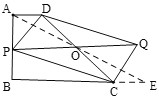
设对角线PQ与DC相交于点O，连接AO并延长AO交BC的延长线于E，根据平行四边形得性质可知点O为CD、PQ的中点，根据平行线的性质可得∠DAE=∠E，利用AAS可证明△AOD≌△EOC，可得AD=CE，可求出BE的长，由垂线段最短可知当OP⊥AB时，OP最短，可得PQ为最小值，由AB⊥BC，可得OP//BC，由OD=OC可得OP为△ABE的中位线，根据三角形中位线的性质可求出OP的长，进而可求出PQ的长．

如图，设对角线PQ与DC相交于点O，连接AO并延长AO交BC的延长线于E，

∵四边形是平行四边形，

∴O是DC、PQ的中点，即OD=OC，OP=OQ，

∵

∴∠DAE=∠E，

在△AOD和△EOC中，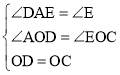

∴△AOD≌△EOC（AAS），

∴，

∵AD=1，BC=3，

∴BE=4，

当OP⊥AB时，OP最短，即PQ有最小值，

∵AB⊥BC，AD//BC，

∴OP//AD//BC，

∴OP为△ABE的中位线，

∴OP=BE=2，

∴PQ=2OP=4，即PQ的最小值为4，

故答案为：4