题目内容
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A(1,3 ),B(4,0)两点.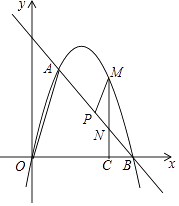
(1)求出抛物线的解析式;
(2)在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN , 求出 ![]() 的值,并求出此时点M的坐标.
的值,并求出此时点M的坐标.
【答案】
(1)解:∵A(1,3),B(4,0)在抛物线y=mx2+nx的图象上,
∴ ![]() ,解得
,解得 ![]() ,
,
∴抛物线解析式为y=﹣x2+4x;
(2)解:存在三个点满足题意,理由如下:
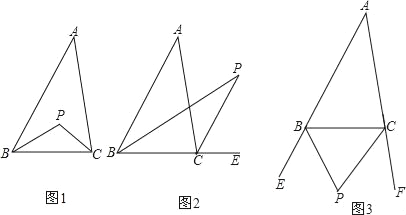
当点D在x轴上时,如图1,过点A作AD⊥x轴于点D,

∵A(1,3),
∴D坐标为(1,0);
当点D在y轴上时,设D(0,d),则AD2=1+(3﹣d)2,BD2=42+d2,且AB2=(4﹣1)2+32=18,
∵△ABD是以AB为斜边的直角三角形,
∴AD2+BD2=AB2,即1+(3﹣d)2+42+d2=18,解得d=4,或d=﹣1
∴D点坐标为(0,4)或(0,﹣1);
综上可知存在满足条件的D点,其坐标为(1,0)或(0,4)或(0,﹣1);
(3)解:如图2,过P作PF⊥CM于点F,
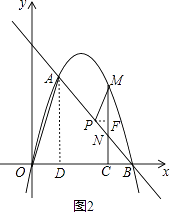
∵PM∥OA,
∴Rt△ADO∽Rt△MFP,
∴ ![]() =
= ![]() =3,
=3,
∴MF=3PF,
在Rt△ABD中,BD=3,AD=3,
∴tan∠ABD=1,
∴∠ABD=45°,设BC=a,则CN=a,
在Rt△PFN中,∠PNF=∠BNC=45°,
∴tan∠PNF= ![]() =1,
=1,
∴FN=PF,
∴MN=MF+FN=4PF,
∵S△BCN=2S△PMN,
∴ ![]() a2=2×
a2=2× ![]() ×4PF2,
×4PF2,
∴a=2 ![]() PF,
PF,
∴NC=a=2 ![]() PF,
PF,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴MN= ![]() NC=
NC= ![]() a,
a,
∴MC=MN+NC=( ![]() +1)a,
+1)a,
∴M点坐标为(4﹣a,( ![]() +1)a),
+1)a),
又M点在抛物线上,代入可得﹣(4﹣a)2+4(4﹣a)=( ![]() +1)a,
+1)a,
解得a=3﹣ ![]() 或a=0(舍去),
或a=0(舍去),
OC=4﹣a= ![]() +1,MC=3+2
+1,MC=3+2 ![]() ,
,
∴点M的坐标为( ![]() +1,3+2
+1,3+2 ![]() ).
).
【解析】(1)利用待定系数法来求解;
(2)分两种情况来求解:点D在x轴上和点D在y轴上.当点D在x轴上时,过点A作AD⊥x轴于点D,易求D点的坐标;当点D在y轴上时,设D(0,d),,在Rt△ABD中利用勾股定理可求得d的值,课的答案;
(3)过P作PF⊥CM于点F,易证Rt△ADO∽Rt△MFP,从而得到MF=3PF,在Rt△ABD中和在Rt△PFN中利用三角函数得出MN=4PF,设BC=a,则CN=a,利用△BCN和△PMN之间的面积关系,进而表示出M的坐标,再根据M点在抛物线上求出a的值,进而得到答案.
【考点精析】根据题目的已知条件,利用勾股定理的概念和相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

【题目】某公司有A、B两种客车,它们的载客量和租金如下表,星星中学根据实际情况,计划用A、B型车共5辆,同时送七年级师生到校基地参加社会实践活动.
A | B | |
载客量(人/辆) | 40 | 20 |
租金(元/辆) | 200 | 150 |
(1)若要保证租金费用不超过980元,请问该学校有哪几种租车方案?
(2)在(1)的条件下,若七年级师生共有150人,问哪种租车方案最省钱?