题目内容
【题目】在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD;
(2)若DE=3,BC=8,求△FCD的面积.
【答案】
(1)证明:∵D是BC的中点,DE⊥BC,
∴BE=CE,
∴∠B=∠DCF,
∵AD=AC,
∴∠FDC=∠ACB,
∴△ABC∽△FCD.
(2)解:过A作AG⊥CD,垂足为G.
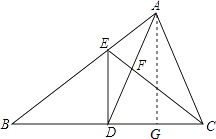
∵AD=AC,
∴DG=CG,
∴BD:BG=2:3,
∵ED⊥BC,
∴ED∥AG,
∴△BDE∽△BGA,
∴ED:AG=BD:BG=2:3,
∵DE=3,
∴AG= ![]() ,
,
∵△ABC∽△FCD,BC=2CD,
∴ ![]() =(
=( ![]() )2=
)2= ![]() .
.
∵S△ABC= ![]() ×BC×AG=
×BC×AG= ![]() ×8×
×8× ![]() =18,
=18,
∴S△FCD= ![]() S△ABC=
S△ABC= ![]() .
.
【解析】(1)先证明∠B=∠DCF和∠FDC=∠ACB,可证得△ABC∽△FCD;
(2)过A作AG⊥CD,垂足为G.先证明△BDE∽△BGA,再由相似三角形的性质求得AG的长,由(1)知△ABC∽△FCD,利用面积比等于相似比的平方可求得△ABC的面积,进而可求得△FCD的面积.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目