ЬтФПФкШн
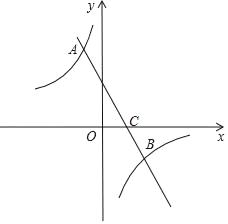
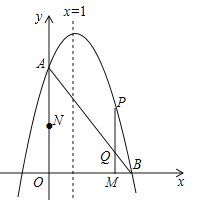
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯп![]() гыyжсЯрНЛгкЕуAЃЈ0ЃЌ3ЃЉЃЌгыxе§АыжсЯрНЛгкЕуBЃЌЖдГЦжсЪЧжБЯпx=1ЃЎ
гыyжсЯрНЛгкЕуAЃЈ0ЃЌ3ЃЉЃЌгыxе§АыжсЯрНЛгкЕуBЃЌЖдГЦжсЪЧжБЯпx=1ЃЎ
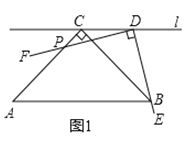
ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФНтЮіЪНвдМАЕуBЕФзјБъЃЎ
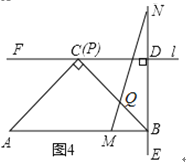
ЃЈ2ЃЉЖЏЕуMДгЕуOГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШбиxжсе§ЗНЯђдЫЖЏЃЌЭЌЪБЖЏЕуNДгЕуOГіЗЂЃЌвдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШбиyжсе§ЗНЯђдЫЖЏЃЌЕБNЕуЕНДяAЕуЪБЃЌMЁЂNЭЌЪБЭЃжЙдЫЖЏЃЎЙ§ЖЏЕуMзїxжсЕФДЙЯпНЛЯпЖЮABгкЕуQЃЌНЛХзЮяЯпгкЕуPЃЌЩшдЫЖЏЕФЪБМфЮЊtУыЃЎ
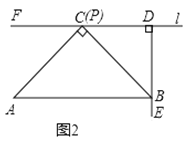
ЂйЕБtЮЊКЮжЕЪБЃЌЫФБпаЮOMPNЮЊОиаЮЃЎ
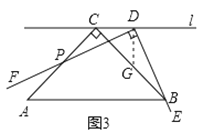
ЂкЕБtЃО0ЪБЃЌЁїBOQФмЗёЮЊЕШбќШ§НЧаЮЃПШєФмЃЌЧѓГіtЕФжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌBЕузјБъЮЊЃЈ3ЃЌ0ЃЉЃЛЃЈ2ЃЉЂйЃЛЂкЃЎ
ЃЌBЕузјБъЮЊЃЈ3ЃЌ0ЃЉЃЛЃЈ2ЃЉЂйЃЛЂкЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЖдГЦжсЙЋЪНПЩЧѓЕУbЃЌгЩAЕузјБъПЩЧѓЕУcЃЌдђПЩЧѓЕУХзЮяЯпНтЮіЪНЃЛдйСюy=0ПЩЧѓЕУBЕузјБъЃЛ
ЃЈ2ЃЉЂйгУtПЩБэЪОГіONКЭOMЃЌдђПЩБэЪОГіPЕузјБъЃЌМДПЩБэЪОГіPMЕФГЄЃЌгЩОиаЮЕФаджЪПЩЕУON=PMЃЌПЩЕУЕНЙигкtЕФЗНГЬЃЌПЩЧѓЕУtЕФжЕЃЛЂкгЩЬтвтПЩжЊOB=OAЃЌЙЪЕБЁїBOQЮЊЕШбќШ§НЧаЮЪБЃЌжЛФмгаOB=BQЛђOQ=BQЃЌгУtПЩБэЪОГіQЕуЕФзјБъЃЌдђПЩБэЪОГіOQКЭBQЕФГЄЃЌЗжБ№ЕУЕНЙигкtЕФЗНГЬЃЌПЩЧѓЕУtЕФжЕЃЎ
ЃЈ1ЃЉЁпХзЮяЯп![]() ЖдГЦжсЪЧжБЯпx=1ЃЌ
ЖдГЦжсЪЧжБЯпx=1ЃЌ
ЁрЉ![]() =1ЃЌНтЕУb=2ЃЌ
=1ЃЌНтЕУb=2ЃЌ
ЁпХзЮяЯпЙ§AЃЈ0ЃЌ3ЃЉЃЌ
Ёрc=3ЃЌ
ЁрХзЮяЯпНтЮіЪНЮЊ![]() ЃЌСюy=0ПЩЕУ
ЃЌСюy=0ПЩЕУ![]() ЃЌНтЕУx=Љ1Лђx=3ЃЌ
ЃЌНтЕУx=Љ1Лђx=3ЃЌ
ЁрBЕузјБъЮЊЃЈ3ЃЌ0ЃЉЃЛ
ЃЈ2ЃЉЂйгЩЬтвтПЩжЊON=3tЃЌOM=2tЃЌ
ЁпPдкХзЮяЯпЩЯЃЌ
ЁрPЃЈ2tЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁпЫФБпаЮOMPNЮЊОиаЮЃЌ
ЁрON=PMЃЌ
Ёр3t=![]() ЃЌНтЕУt=1Лђt=Љ
ЃЌНтЕУt=1Лђt=Љ![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
ЁрЕБtЕФжЕЮЊ1ЪБЃЌЫФБпаЮOMPNЮЊОиаЮЃЛ
ЂкЁпAЃЈ0ЃЌ3ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌ
ЁрOA=OB=3ЃЌЧвПЩЧѓЕУжБЯпABНтЮіЪНЮЊy=Љx+3ЃЌ
ЁрЕБtЃО0ЪБЃЌOQЁйOBЃЌ
ЁрЕБЁїBOQЮЊЕШбќШ§НЧаЮЪБЃЌгаOB=QBЛђOQ=BQСНжжЧщПіЃЌгЩЬтвтПЩжЊOM=2tЃЌ
ЁрQЃЈ2tЃЌЉ2t+3ЃЉЃЌ
ЁрOQ=![]() ЃЌBQ=
ЃЌBQ=![]() |2tЉ3|ЃЌгжгЩЬтвтПЩжЊ0ЃМtЃМ1ЃЌЕБOB=QBЪБЃЌдђга
|2tЉ3|ЃЌгжгЩЬтвтПЩжЊ0ЃМtЃМ1ЃЌЕБOB=QBЪБЃЌдђга![]() |2tЉ3|=3ЃЌНтЕУt=
|2tЉ3|=3ЃЌНтЕУt=![]() ЃЈЩсШЅЃЉЛђt=
ЃЈЩсШЅЃЉЛђt=![]() ЃЛ
ЃЛ
ЕБOQ=BQЪБЃЌдђга![]() =
=![]() |2tЉ3|ЃЌНтЕУt=
|2tЉ3|ЃЌНтЕУt=![]() ЃЛ
ЃЛ
злЩЯПЩжЊЕБtЕФжЕЮЊ![]() Лђ
Лђ![]() ЪБЃЌЁїBOQЮЊЕШбќШ§НЧаЮЃЎ
ЪБЃЌЁїBOQЮЊЕШбќШ§НЧаЮЃЎ

 ИпаЇжЧФмПЮЪБзївЕЯЕСаД№АИ
ИпаЇжЧФмПЮЪБзївЕЯЕСаД№АИ НнОЖбЕСЗМьВтОэЯЕСаД№АИ
НнОЖбЕСЗМьВтОэЯЕСаД№АИ