题目内容
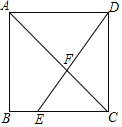
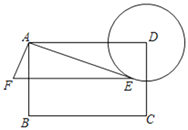
【题目】如图，矩形ABCD中，AB＝6，BC＝9，以D为圆心，3为半径作⊙D，E为⊙D上一动点，连接AE，以AE为直角边作Rt△AEF，使∠EAF＝90°，tan∠AEF＝
，则点F与点C的最小距离为_____．
【答案】3
﹣1 ．
【解析】
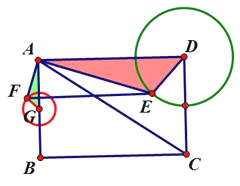
如图，取AB的中点G，连接FG，根据已知条件易证△AFG∽△EAD，根据相似三角形的性质求得FG=1；即可得点F在以点G为圆心，半径为1的圆上，所以当点F在线段GC上时，点F与点C的距离最小，由此即可求得点F与点C的最小距离.
如图，取AB的中点G，连接FG，
∵AB=4，AD=6，
∴AG=2，
；
在Rt△AEF，∠EAF＝90°，tan∠AEF＝
，
∴
,
∴
,
∵∠EAF＝∠BAD＝90°，
∴∠FAG＝∠EAD，
∴△AFG∽△EAD，
∴
,
∵DE=3,
∴FG=1；
∵点E为⊙D上一动点，
∴点F在以点G为圆心，半径为1的圆上，
∴当点F在线段GC上时，点F与点C的距离最小，
在Rt△GBC中，BC=6，GB=3，由勾股定理求得GC=3，
∴FC=3﹣1．
即点F与点C的最小距离为3﹣1．
故答案为：3﹣1．
练习册系列答案
全能测控期末小状元系列答案
相关题目
