题目内容
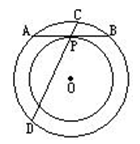
如图,△ABC内接于半圆,AB为直径,设D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F.
求证:FD=FG.
求证:FD=FG.

见解析
试题分析:由D是弧AC的中点可得弧AD=弧DC,即得∠ABD=∠DBC,根据AB为直径再结合DE⊥AB可得∠EDG=∠DGF,即可证得结论.
∵D是弧AC的中点,
∴弧AD=弧DC,
∴∠ABD="∠DBC"
∵AB为直径
∴∠ACB=90°
∴∠CGB=90°-∠CBA,
∵∠DGF=∠CGB(对顶角相等),
∴∠DGF=90°-∠CBD,
∵DE⊥AB,
∴∠GDF=90°-∠DBE,
∴∠EDG=∠DGF,
∴△FDG是等腰△,
∴FD=FG.
点评:解答本题的关键是熟练掌握圆周角定理的推论:直径所对的圆周角是直角.

练习册系列答案
相关题目
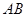 是
是 的直径,弦
的直径,弦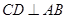 ,垂足为
,垂足为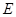 ,
,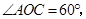
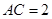 .
.
 的长;
的长;

 上,让纸片ABCD按上述方法旋转,请直接写出经过多少次旋转,顶点A经过的路程是
上,让纸片ABCD按上述方法旋转,请直接写出经过多少次旋转,顶点A经过的路程是 .
.