题目内容

已知：如图，正方形ABCD的边长为9，M在BC上，MC=6，在AC上找一个点P，使BP+MP最小值，求出最小值为多少？（要求画出图形，进行计算，不要求证明）
分析：连接BD、MD，由正方形的性质可知B、D两点关于直线AC对称，故DM的长即为BP+MP的最小值，再由勾股定理求出DM的长即可．
解答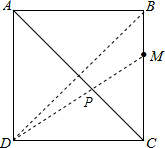：解：连接BD、MD，
∵四边形ABCD是正方形，
∴B、D两点关于直线AC对称，
∴DM的长即为BP+MP的最小值，
在Rt△CDM中，
∵MC=6，CD=9，
∴DM=
MC2+CD2
=
62+92
=3
13
．
答：最小值为3
13
．
点评：本题考查的是轴对称-最短路线问题及正方形的性质，根据题意作出辅助线，利用勾股定理求解是解答此题的关键．
练习册系列答案
相关题目
已知：如图，O正方形ABCD的中心，BE平分∠DBC，交DC于点E，延长BC到点F，使CF=CE精英家教网，连接DF，交BE的延长线于点G，连接OG．
（1）求证：△BCE≌△DCF；
（2）OG与BF有什么数量关系？证明你的结论；
（3）若GE•GB=4-2
2
，求正方形ABCD的面积．
已知，如图在正方形OADC中，点C的坐标为（0，4），点A的坐标为（4，0），CD的延长线交双曲线y=
32
x
于点B．
（1）求直线AB的解析式；精英家教网
精英家教网
（2）G为x轴的负半轴上一点连接CG，过G作GE⊥CG交直线AB于E．求证CG=GE；
（3）在（2）的条件下，延长DA交CE的延长线于F，当G在x的负半轴上运动的过程中，请问
OG+GF
DF
的值是否为定值，若是，请求出其值；若不是，请说明你的理由．
精英家教网
24、已知，如图：正方形ABCD，将Rt△EFG斜边EG的中点与点A重合，直角顶点F落在正方形的AB边上，Rt△EFG的两直角边分别交AB、AD边于P、Q两点，（点P与点F重合），如图所示：

（1）求证：EP2+GQ2=PQ2；
（2）若将Rt△EFG绕着点A逆时针旋转α（0°＜α≤90°），两直角边分别交AB、AD边于P、Q两点，如图2所示：判断四条线段EP、PF、FQ、QG之间是否存在什么确定的相等关系？若存在，证明你的结论．若不存在，请说明理由；
（3）若将Rt△EFG绕着点A逆时针旋转α（90°＜α＜180°），两直角边分别交AB、AD两边延长线于P、Q两点，并判断四条线段EP、PF、FQ、QG之间存在何种确定的相等关系？按题意完善图3，请直接写出你的结论（不用证明）．
已知：如图，正方形ABCD的边长为2a，H是以BC为直径的半圆O上一点，过H与圆O相切的直线交AB精英家教网于E，交CD于F．
（1）当点H在半圆上移动时，切线EF在AB、CD上的两个交点也分别在AB、CD上移动（E、A不重合，F、D不重合），试问：四边形AEFD的周长是否也在变化？证明你的结论；
（2）设△BOE的面积为S1，△COF的面积为S2，正方形ABCD的面积为S，且S1+S2=
1348
S，求BE与CF的长．
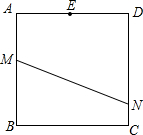已知：如图，正方形纸片ABCD的边长是4，点M、N分别在两边AB和CD上（其中点N不与点C重合），沿直线MN折叠该纸片，点B恰好落在AD边上点E处．
（1）设AE=x，四边形AMND的面积为 S，求 S关于x 的函数解析式，并指明该函数的定义域；
（2）当AM为何值时，四边形AMND的面积最大？最大值是多少？
（3）点M能是AB边上任意一点吗？请求出AM的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网