题目内容
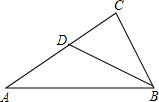 如图,D是△ABC中AC边上的一点,根据下列条件不可推出△BDC∽△ABC的是
如图,D是△ABC中AC边上的一点,根据下列条件不可推出△BDC∽△ABC的是
- A.∠A=∠DBC
- B.∠ABC=∠BDC
- C.BC2=AC•DC
- D.AB•CD=BC•BD
D
分析:由∠C是公共角,根据三边法:三组对应边的比相等的两个三角形相似;两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似,即可求得答案,注意排除法在解选择题中的应用.
解答:∵∠C是公共角,
∴A当∠A=∠DBC时,△BDC∽△ABC;故本选项正确;
当∠ABC=∠BDC时,△BDC∽△ABC;故本选项正确;
C、当BC2=AC•DC,即CD:BC=BC:AC时,△BDC∽△ABC,故本选项正确;
D、当AB•CD=BC•BD,即CD:BC=BD:AB时,不能判定△BDC∽△ABC,故本选项错误.
故选D.
点评:此题考查了相似三角形的判定.此题难度不大,注意熟记定理是关键,注意数形结合思想的应用.
分析:由∠C是公共角,根据三边法:三组对应边的比相等的两个三角形相似;两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似,即可求得答案,注意排除法在解选择题中的应用.
解答:∵∠C是公共角,
∴A当∠A=∠DBC时,△BDC∽△ABC;故本选项正确;
当∠ABC=∠BDC时,△BDC∽△ABC;故本选项正确;
C、当BC2=AC•DC,即CD:BC=BC:AC时,△BDC∽△ABC,故本选项正确;
D、当AB•CD=BC•BD,即CD:BC=BD:AB时,不能判定△BDC∽△ABC,故本选项错误.
故选D.
点评:此题考查了相似三角形的判定.此题难度不大,注意熟记定理是关键,注意数形结合思想的应用.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 8、如图,DE是△ABC中边AC的垂直平分线,若BC=18cm,AB=10cm,则△ABD的周长为( )
8、如图,DE是△ABC中边AC的垂直平分线,若BC=18cm,AB=10cm,则△ABD的周长为( ) 13、如图,AD是△ABC中BC边上的中线,E,F分别是AD、BE的中点,若△BFD的面积为6,则△ABC的面积等于
13、如图,AD是△ABC中BC边上的中线,E,F分别是AD、BE的中点,若△BFD的面积为6,则△ABC的面积等于 如图,D是△ABC中AC边上的一点,根据下列条件不可推出△BDC∽△ABC的是( )
如图,D是△ABC中AC边上的一点,根据下列条件不可推出△BDC∽△ABC的是( ) 如图,D是△ABC中BC边上一点,AB=AC=BD,AD=DC,则∠B的度数是( )
如图,D是△ABC中BC边上一点,AB=AC=BD,AD=DC,则∠B的度数是( ) 如图,P是△ABC中∠B,∠C两角平分线的交点,过点P作DE∥BC,分别与AB、AC交于点D、E,DE=10,则DB+EC=
如图,P是△ABC中∠B,∠C两角平分线的交点,过点P作DE∥BC,分别与AB、AC交于点D、E,DE=10,则DB+EC=