题目内容
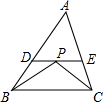如图，P是△ABC中∠B，∠C两角平分线的交点，过点P作DE∥BC，分别与AB、AC交于点D、E，DE=10，则DB+EC=10
10
．分析：根据平行线的性质得∠1=∠2，而DE∥BC，根据平行线的性质得∠2=∠3，得到∠1=∠3，根据等腰三角形的判定得DB=DP，同理可得EC=EP，则DB+EC=DP+PE=DE=10．
解答：
解：如图，
∵PB平分∠ABC，
∴∠1=∠2，
又∵DE∥BC，
∴∠2=∠3，
∴∠1=∠3，
∴DB=DP，
同理可得EC=EP，
∴DB+EC=DP+PE=DE，
而DE=10，
∴DB+EC=10．
故答案为10．
解：如图，∵PB平分∠ABC，
∴∠1=∠2，
又∵DE∥BC，
∴∠2=∠3，
∴∠1=∠3，
∴DB=DP，
同理可得EC=EP，
∴DB+EC=DP+PE=DE，
而DE=10，
∴DB+EC=10．
故答案为10．
点评：本题考查了等腰三角形的判定与性质：有两个角相等的三角形是等腰三角形；等腰三角形的两腰相等．也考查了角平分线的定义以及平行线的性质．
练习册系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
8、如图，DE是△ABC中边AC的垂直平分线，若BC=18cm，AB=10cm，则△ABD的周长为（ ）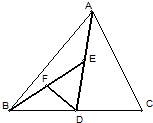
13、如图，AD是△ABC中BC边上的中线，E，F分别是AD、BE的中点，若△BFD的面积为6，则△ABC的面积等于
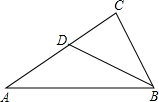如图，D是△ABC中AC边上的一点，根据下列条件不可推出△BDC∽△ABC的是（ ）
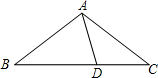如图，D是△ABC中BC边上一点，AB=AC=BD，AD=DC，则∠B的度数是（ ）