Question

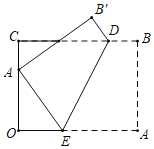
【题目】如图，矩形OABC中，OA＝4，AB＝3，点D在边BC上，且CD＝3DB，点E是边OA上一点，连接DE，将四边形ABDE沿DE折叠，若点A的对称点A′恰好落在边OC上，则OE的长为（　　）

A.B.C.D.1

Answer 1

【答案】B

【解析】

连接A′D，AD，根据矩形的性质得到BC＝OA＝4，OC＝AB＝3，∠C＝∠B＝∠O＝90°，求得CD＝3，BD＝1，根据折叠的得到A′D＝AD，A′E＝AE，根据全等三角形的性质得到A′C＝BD＝1，根据勾股定理即可得到结论．

解：连接A′D，AD，

∵四边形OABC是矩形，

∴BC＝OA＝4，OC＝AB＝3，∠C＝∠B＝∠O＝90°，

∵CD＝3DB，

∴CD＝3，BD＝1，

∴CD＝AB，

∵将四边形ABDE沿DE折叠，若点A的对称点A′恰好落在边OC上，

∴A′D＝AD，A′E＝AE，

在Rt△A′CD与Rt△DBA中，，

∴Rt△A′CD≌Rt△DBA（HL），

∴A′C＝BD＝1，

∴A′O＝2，

∵A′O2+OE2＝A′E2，

∴22+OE2＝（4﹣OE）2，

∴

故选：B．