题目内容
【题目】如图，在矩形ABCD中，AB＝12，BC＝10，M是AD边的中点，N是AB边上的动点，将△AMN沿MN所在直线折叠，得到△
，连接
，则的最小值是__________．
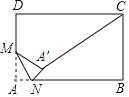
【答案】8
【解析】
由折叠的性质可得AM＝A'M＝1，可得点A'在以点M为圆心，AM为半径的圆上，当点A'在线段MC上时，A'C有最小值，由勾股定理可求MC的长，即可求A′C的最小值．
∵四边形ABCD是矩形
∴AB＝CD＝12，BC＝AD＝10，
∵M是AD边的中点，
∴AM＝MD＝5
∵将△AMN沿MN所在直线折叠，
∴AM＝A'M＝5
∴点A'在以点M为圆心，AM为半径的圆上，
∴如图，当点A'在线段MC上时，A'C有最小值，
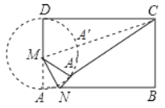
∵MC＝
=13
∴A′C的最小值＝MCMA'＝13-5=8
故答案为：8．
练习册系列答案
相关题目
【题目】某服装店计划购进一批甲、乙两种款式的运动服进行销售，进价和售价如下表所示：
运动服款式 | 甲 | 乙 |
进价（元/套） | 80 | 100 |
售价（元/套） | 120 | 160 |
若购进两种款式的运动服共300套，且投入资金不超过26800元．
（1） 该服装店应购进甲款运动服至少多少套？
（2）若服装店购进甲款运动服的进价每套降低a元，并保持这两款运动服的售价不变，且最多购进240套甲款运动服．如果这批运动服售出后，服装店刚好获利18480元，求a的取值范围．
