题目内容
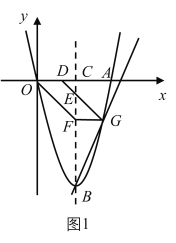
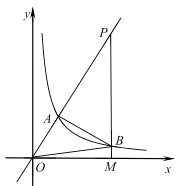
【题目】如图1,抛物线y=﹣x2+bx+c(a≠0)的顶点为C,交x轴于A![]() 、B
、B![]() 两点,交y轴于点D.
两点,交y轴于点D.
(1)求抛物线的解析式;并直接写出点C的坐标.
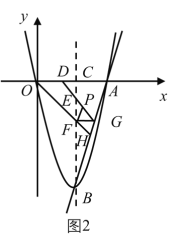
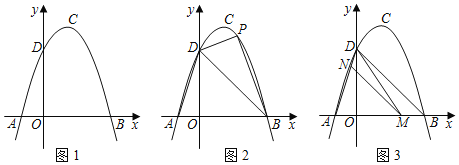
(2)如图2,点P为直线BD上方抛物线上一点,作PE⊥BD于点E,AF⊥BD于点F若![]() ,请求出点P的坐标.
,请求出点P的坐标.
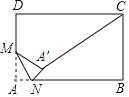
(3)如图3,M为线段AB上的一点,过点M作MN∥BD,交线段AD于点N,连接MD,若△DNM∽△BMD,请求出点M的坐标.
【答案】(1)![]() ,(1,4);(2)(1,4)或(2,3);(3)(
,(1,4);(2)(1,4)或(2,3);(3)(![]() ,0).
,0).
【解析】
(1)把点A、B代入解析式,利用待定系数法求解,即可得到答案;
(2)由![]() ,得到
,得到![]() ,然后求出直线BD的解析式,设P(m,﹣m2+2m+3),则Q(m,﹣m+3),则
,然后求出直线BD的解析式,设P(m,﹣m2+2m+3),则Q(m,﹣m+3),则![]() ,即可求出点P的坐标;
,即可求出点P的坐标;
(3)设M(a,0),证明△AMN∽△ABD,可得![]() ,再由△DNM∽△BMD,可得
,再由△DNM∽△BMD,可得![]() ,得出关于a的方程,解方程即可得出答案.
,得出关于a的方程,解方程即可得出答案.
解:(1)∵抛物线y=ax2+bx+c(a≠0)过A(﹣1,0)B(3,0)
设解析式![]() ,
,
∴抛物线的解析式为:![]() .
.
∴顶点C的坐标(1,4);
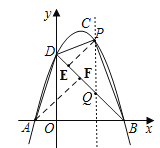
(2)作PE⊥BD于点E,AF⊥BD于点F,
若![]() ,则
,则![]() ,
,
∴S△PBD = ![]() S△ABD=
S△ABD=![]() ×6=3
×6=3
过点P作PQ∥y轴交DB于点Q,
∵抛物线的解析式为y=﹣x2+2x+3
∴D(0,3).
设直线BD的解析式为y=kx+n,
∴![]() ,解得:
,解得:![]() ,
,
∴直线BD的解析式为y=﹣x+3.
设P(m,﹣m2+2m+3),则Q(m,﹣m+3),
∴PQ=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m.
∵S△PBD=S△PQD+S△PQB,
∴S△PBD=![]() ×PQ×(3﹣m)=
×PQ×(3﹣m)=![]() PQ=﹣
PQ=﹣![]() m,
m,
∵S△PBD=3,
∴﹣![]() m=3.
m=3.
解得:m1=1,m2=2.
∴点P的坐标为(1,4)或(2,3).
(3)∵B(3,0),D(0,3),
∴BD=![]() =3
=3![]() ,
,
设M(a,0),
∵MN∥BD,
∴△AMN∽△ABD,
∴![]() ,即
,即![]() .
.
∴MN=![]() (1+a),DM=
(1+a),DM=![]() =
=![]() ,
,
∵△DNM∽△BMD,
∴![]() ,
,
∴DM2=BDMN,
∴9+a2=3![]() (1+a).
(1+a).
解得:a=![]() 或a=3(舍去).
或a=3(舍去).
∴点M的坐标为(![]() ,0).
,0).

 名校课堂系列答案
名校课堂系列答案【题目】农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克) | 30 | 35 | 40 | 45 | 50 |
日销售量p(千克) | 600 | 450 | 300 | 150 | 0 |
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式;
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若农经公司每销售1千克这种农产品需支出a元(a>0)的相关费用,当40≤x≤45时,农经公司的日获利的最大值为2430元,求a的值.(日获利=日销售利润﹣日支出费用)