题目内容
已知:二次函数y=2x2-4x+m-1,则它的图象对称轴为直线分析:①根据公式法求对称轴.②把(-1,1)代入函数,可求m的值,从而得到函数解析式,再次利用公式法可求函数最小值,即是函数最低点的纵坐标.
解答:解:①∵-
=-
=1,
∴对称轴是x=1;
②把(-1,1)代入二次函数得2+4+m-1=1,解得m=-4,
∴函数的解析式就是y=2x2-4x-5,
∴-
=-
=-7.
即函数最小值就是-7,
故答案为x=1,-7.
| b |
| 2a |
| -4 |
| 2×2 |
∴对称轴是x=1;
②把(-1,1)代入二次函数得2+4+m-1=1,解得m=-4,
∴函数的解析式就是y=2x2-4x-5,
∴-
| 4ac-b2 |
| 4a |
| 4×2×(-5)-(-4)2 |
| 4×2 |
即函数最小值就是-7,
故答案为x=1,-7.
点评:本题主要考查二次函数的最值和二次函数的性质的知识点,解答本题的关键是用公式法求出y=ax2+bx+c的顶点坐标为
(-
,
),对称轴是x=-
.
(-
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案
相关题目
 已知:二次函数的表达式为y=2x2+4x-1.
已知:二次函数的表达式为y=2x2+4x-1.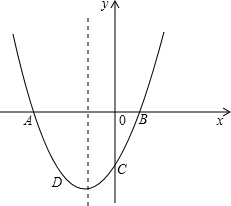 交于点C,点D(-2,-3)在抛物线上.
交于点C,点D(-2,-3)在抛物线上.