题目内容
若两个相似三角形的面积之比为1:4，则它们的周长之比为（ ）
| A． 1:2 | B． 1:4 | C． 1:5 | D．1:16 |
A.
解析试题分析：根据相似三角形的性质，相似三角形的面积之比等于相似比的平方，利用面积之比是1:4，求出相似比，然后再根据相似三角形的周长之比等于相似比，即可求出它们的相似比.
∵两个相似三角形的面积之比是1:4，
∴两个相似三角形的相似比是1:2.
∴两个相似三角形的周长之比是1:2.
故选择A.
考点：相似三角形的性质.
练习册系列答案
相关题目
如图，在△ABC中，若DE∥BC，AD=5，BD=10，DE=4，则BC的值为( )
| A．8 | B．9 | C．10 | D．12 |
如图，为估算某河的宽度，在河对岸选定一个目标点A，在近岸取点B，C，D，使得AB⊥BC，CD⊥BC，点E在BC上，且点A，E，D在同一条直线上．若测得BE=20m，CE=10m，CD=20m，则河的宽度AB等于（ ）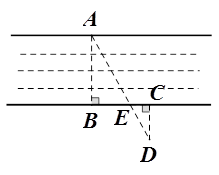
| A．30m | B．60m | C．20m | D．40m |
若x：y=6：5，则下列等式中不正确的是（ ）
A． | B． | C． | D． |
△ABC∽△A′B′C′，如果∠A=55°，∠B=100°，则∠C′的度数等于（ ）
| A．55° | B．100° | C．25° | D．30° |
如图，在△
中，
为
边上一点，∠
∠
，
，
，则
的长为（ ）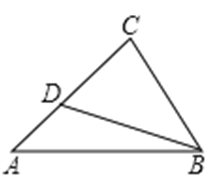
| A．1 | B．4 | C．3 | D．2 |
