题目内容
（2013年四川眉山3分）如图，∠BAC=∠DAF=90°，AB=AC，AD=AF，点D、E为BC边上的两点，且∠DAE=45°，连接EF、BF，则下列结论：①△AED≌△AEF；②△ABE∽△ACD；③BE+DC＞DE；④BE2+DC2=DE2，
其中正确的有【 】个．
A．1 B．2 C．3 D．4
C。
解析
练习册系列答案
名校课堂系列答案
相关题目
若两个相似三角形的面积之比为1:4，则它们的周长之比为（ ）
| A． 1:2 | B． 1:4 | C． 1:5 | D．1:16 |
已知△ABC∽△DEF，若△ABC与△DEF的相似比为3：4，则△ABC与△DEF的面积比为（ ）
| A．4：3 | B．3：4 | C．16：9 | D．9：16 |
小明在测量楼高时，先测出楼房落在地面上的影长BA为15米（如图），然后在A处树立一根高2米的标杆，测得标杆的影长AC为3米，则楼高为
| A．10米 | B．12米 | C．15米 | D．22.5米 |
如图所示，在平行四边形ABCD中，AC与BD相交于点O，E为OD的中点，连接AE并延长交DC于点F，则DF：FC=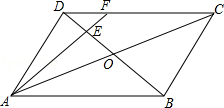
| A．1：4 | B．1：3 | C．2：3 | D．1：2 |
如图，∠ABD=∠BDC=90°，∠A=∠CBD，AB=3，BD=2，则CD的长为
A． | B． | C．2 | D．3 |
，则△CEF的周长是 ．
如图，在平行四边形ABCD中，点E在AD上，连接CE并延长与BA的延长线交于点F，若AE=2ED，CD=3cm，则AF的长为【 】
| A．5cm | B．6cm | C．7cm | D．8cm |