题目内容
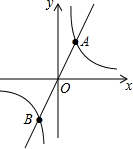 如图,反比例函数y=
如图,反比例函数y=| k |
| x |
| k |
| x |
-1≤x<0或x≥1
-1≤x<0或x≥1
.分析:把A((m,2)、B(-m,-2)代入y=2x求出m的值,得出A、B的坐标,根据A、B的坐标结合图象求出即可.
解答:解:∵反比例函数y=
的图象与一次函数y=2x的图象相交于点A(m,2)、B(-m,-2)两点,
∴把A((m,2)、B(-m,-2)代入y=2x得:m=1,
即A(1,2),B(-1,-2),
∴不等式2x≥
的解集是-1≤x<0或x≥1,
故答案为:-1≤x<0或x≥1.
| k |
| x |
∴把A((m,2)、B(-m,-2)代入y=2x得:m=1,
即A(1,2),B(-1,-2),
∴不等式2x≥
| k |
| x |
故答案为:-1≤x<0或x≥1.
点评:本题考查了反比例函数与一次函数的交点问题,函数的图象的应用,主要考查学生的计算能力和观察图象的能力,用了数形结合思想.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
 如图,反比例函数y=
如图,反比例函数y= 如图,反比例函数
如图,反比例函数 如图,反比例函数
如图,反比例函数 如图,反比例函数
如图,反比例函数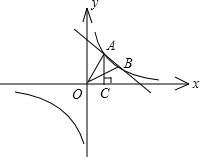 如图,反比例函数
如图,反比例函数