题目内容
【题目】如图,已知BD为△ABC的角平分线,请按如下要求操作解答:
(1)过点D画DE∥BC交AB于E,若∠A=68°,∠AED=42°,求∠BDC的度数.
(2)画△ABC的角平分线CF交BD于点M,若∠A=60°,求∠CMD的度数.

【答案】(1)89°;(2)60°.
【解析】
(1)过点D作DE∥BC交AB于点E,由DE∥BC可知∠AED=∠ABC=42°,所以∠DBC=![]() ∠ABC=21°,从而可求出∠C=180°-∠ABC-∠A=70°,∠BDC=180°
∠ABC=21°,从而可求出∠C=180°-∠ABC-∠A=70°,∠BDC=180°![]() ∠DBC
∠DBC![]() ∠C=89°;(2)因为∠A=60°,所以∠ABC+∠ACB=120°,由于BD平分∠ABC,CF平分∠ACB,所以∠MBC+∠MCB=60°,即∠CMD=60°.
∠C=89°;(2)因为∠A=60°,所以∠ABC+∠ACB=120°,由于BD平分∠ABC,CF平分∠ACB,所以∠MBC+∠MCB=60°,即∠CMD=60°.
(1)过点D作DE∥BC交AB于点E,
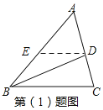
∵DE∥BC,
∴∠AED=∠ABC=42°,
∵BD平分∠ABC,
∴∠DBC=![]() ∠ABC=21°,
∠ABC=21°,
∴∠C=180°![]() ∠ABC
∠ABC![]() ∠A=70°,
∠A=70°,
∴∠BDC=180°![]() ∠DBC
∠DBC![]() ∠C=89°;
∠C=89°;
(2)作△ABC的角平分线CF交BD于点M,
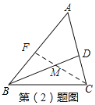
∵∠A=60°,
∴∠ABC+∠ACB=120°,
∴BD平分∠ABC,CF平分∠ACB,
∴∠CMD=∠MBC+∠MCB=![]() (∠ABC+∠ACB)=60°.
(∠ABC+∠ACB)=60°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目







