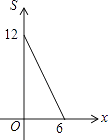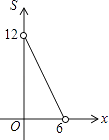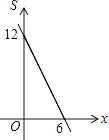ЬтФПФкШн
ЁОЬтФПЁПШчЭМ1ЃЌНЋ![]() жНЦЌбижаЮЛЯп
жНЦЌбижаЮЛЯп![]() елЕўЃЌЪЙЕу
елЕўЃЌЪЙЕу![]() ЕФЖдГЦЕу
ЕФЖдГЦЕу![]() Тфдк
Тфдк![]() БпЩЯЃЌдйНЋжНЦЌЗжБ№биЕШбќ
БпЩЯЃЌдйНЋжНЦЌЗжБ№биЕШбќ![]() КЭЕШбќ
КЭЕШбќ![]() ЕФЕзБпЩЯЕФИпЯп
ЕФЕзБпЩЯЕФИпЯп![]() ЃЌ
ЃЌ![]() елЕўЃЌелЕўКѓЕФШ§ИіШ§НЧаЮЦДКЯаЮГЩвЛИіОиаЮЃЌРрЫЦЕиЃЌЖдЖрБпаЮНјааелЕўЃЌШєЗелКѓЕФЭМаЮЧЁФмЦДГЩвЛИіЮоЗьЯЖЁЂЮожиЕўЕФОиаЮЃЌетбљЕФОиаЮГЦЮЊЕўКЯОиаЮЃЎ
елЕўЃЌелЕўКѓЕФШ§ИіШ§НЧаЮЦДКЯаЮГЩвЛИіОиаЮЃЌРрЫЦЕиЃЌЖдЖрБпаЮНјааелЕўЃЌШєЗелКѓЕФЭМаЮЧЁФмЦДГЩвЛИіЮоЗьЯЖЁЂЮожиЕўЕФОиаЮЃЌетбљЕФОиаЮГЦЮЊЕўКЯОиаЮЃЎ
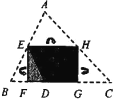
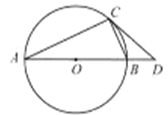
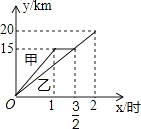
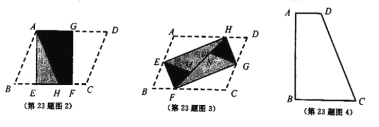
(1)НЋ![]() жНЦЌАДЭМ2ЕФЗНЪНелЕўГЩвЛИіЕўКЯОиаЮ
жНЦЌАДЭМ2ЕФЗНЪНелЕўГЩвЛИіЕўКЯОиаЮ![]() ЃЌдђВйзїаЮГЩЕФелКлЗжБ№ЪЧЯпЖЮ_____ЃЌ_____ЃЛ
ЃЌдђВйзїаЮГЩЕФелКлЗжБ№ЪЧЯпЖЮ_____ЃЌ_____ЃЛ![]() ______.
______.
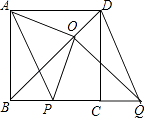
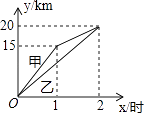
(2)![]() жНЦЌЛЙПЩвдАДЭМ3ЕФЗНЪНелЕўГЩвЛИіЕўКЯОиаЮ
жНЦЌЛЙПЩвдАДЭМ3ЕФЗНЪНелЕўГЩвЛИіЕўКЯОиаЮ![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
(3)ШчЭМ4ЃЌЫФБпаЮ![]() жНЦЌТњзу
жНЦЌТњзу![]() ЃЎаЁУїАбИУжНЦЌелЕўЃЌЕУЕНЕўКЯе§ЗНаЮЃЎЧыФуАяжњЛГіЕўКЯе§ЗНаЮЕФЪОвтЭМЃЌВЂЧѓГі
ЃЎаЁУїАбИУжНЦЌелЕўЃЌЕУЕНЕўКЯе§ЗНаЮЃЎЧыФуАяжњЛГіЕўКЯе§ЗНаЮЕФЪОвтЭМЃЌВЂЧѓГі![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃЈ1ЃЉAEЃЛGFЃЛ1:2ЃЛЃЈ2ЃЉ13ЃЛЃЈ3ЃЉАДЭМ1ЕФелЗЈЃЌдђAD=1ЃЌBC=7ЃЛАДЭМ2ЕФелЗЈЃЌдђAD=![]() ,BC=
,BC=![]() .
.
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉгЩЭМ2ЙлВьПЩЕУГіД№АИЮЊAE,GF,гЩелЕўЕФжсЖдГЦаджЪПЩЕУГіД№АИЮЊ1ЃК2ЃЛЃЈ2ЃЉгЩEFКЭEHЕФГЄЖШИљОнЙДЙЩЖЈРэПЩЧѓГіFHЕФГЄЖШЃЌдйгЩелЕўЕФжсЖдГЦаджЪвзжЄЁїAEHЁеЁїCGFЃЛдйИљОнШЋЕШШ§НЧаЮЕФаджЪПЩЕУГіADЕФГЄЖШЃЛЃЈ3ЃЉгЩелЕўЕФЭМПЩЗжБ№ЧѓГіADКЭBCЕФГЄЖШ.
ЪдЬтНтЮіЃКЃЈ1ЃЉAEЃЛGFЃЛ1:2
ЃЈ2ЃЉНтЃКЁпЫФБпаЮEFGHЪЧЕўКЯОиаЮЃЌЁЯFEH=90Ёу,EF=5,EH=12;
ЁрFH=![]() =13;
=13;
гЩелЕўЕФжсЖдГЦадПЩжЊЃКDH=NH,AH=HM,CF=FN;
взжЄЁїAEHЁеЁїCGF;
ЁрCF=AH;
ЁрAD=DH+AH=HN+FN=FH=13.
ЃЈ3ЃЉНтЃКБОЬтгавдЯТСНжжЛљБОелЗЈЃЌШчЭМ1ЃЌЭМ2ЫљЪО.
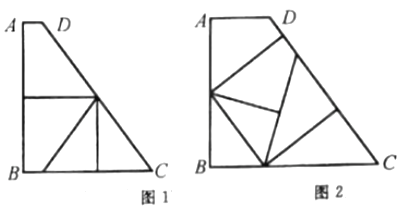
АДЭМ1ЕФелЗЈЃЌдђAD=1ЃЌBC=7.
АДЭМ2ЕФелЗЈЃЌдђAD=![]() ,BC=
,BC=![]() .
.