题目内容
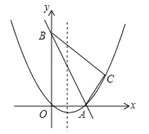
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(1,6),B(3,n)两点.
的图象交于A(1,6),B(3,n)两点.
(1)求反比例函数和一次函数的表达式;
(2)根据图象写出不等式kx+b﹣![]() >0的解集;
>0的解集;
(3)若点M在x轴上、点N在y轴上,且以M、N、A、B为顶点的四边形是平行四边形,请直接写出点M、N的坐标.

【答案】(1)反比例函数解析为y=![]() ,一次函数解析式为y=﹣2x+8;(2)解集为1<x<3或x<0;(3)以M、N、A、B为顶点的四边形是平行四边形时,M(﹣2,0),N(0,﹣4)或M(4,0),N(0,8).
,一次函数解析式为y=﹣2x+8;(2)解集为1<x<3或x<0;(3)以M、N、A、B为顶点的四边形是平行四边形时,M(﹣2,0),N(0,﹣4)或M(4,0),N(0,8).
【解析】试题分析:(1)由A点坐标可求得m的值,可求得反比例函数解析式,则可求得B点坐标,由A、B两点坐标,利用待定系数法可求得直线AB的解析式;
(2)结合函数图象可知不等式的解集即为一次函数图象在反比例函数图象上方时对应的x的取值范围,结合A、B坐标可求得答案;
(3)当AB为平行四边形的边时,①当M在x轴正半轴,N在y轴正半轴时,过A作AC∥y轴,过B作BC∥x轴,可证明△ABC≌△NMO,则可求得OM和ON,②当M在x轴负半轴,N在y轴负半轴时,同理可求得OM和ON的长,则可求得M、N的坐标;当AB为对角线时,可求得M、N、A、B四点共线,不合题意.
试题解析:(1)反比例函数y=![]() 的图象过A(1,6),
的图象过A(1,6),
∴m=1×6=6,
∴反比例函数解析为y=![]() ,
,
把x=3代入可得n=2,
∴B(3,2),
设直线AB解析式为y=kx+b,
把A、B坐标代入可得![]() ,解得
,解得![]() ,
,
∴一次函数解析式为y=﹣2x+8;
(2)不等式kx+b﹣![]() >0可化为不等式kx+b>
>0可化为不等式kx+b>![]() ,
,
即直线在反比例函数图象上方时所对应的自变量x的取值范围,
∵A(1,6),B(3,2),
∴不等式kx+b﹣![]() >0的解集为1<x<3或x<0;
>0的解集为1<x<3或x<0;
(3)当AB为平行四边形的边时,
①当M在x轴正半轴,N在y轴正半轴时,如图1,过A作AC∥y轴,过B作BC∥x轴,
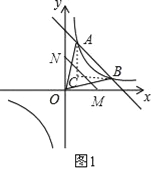
∵A(1,6),B(3,2),
∴BC=3﹣1=2,AC=6﹣2=4,
∵MN∥AB,且MN=AB,
∴∠ONM=∠CAB,
在△NOM和△ACB中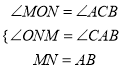 ,
,
∴△NOM≌△ACB(AAS),
∴OM=BC=2,ON=AC=4,
∴M(2,0),N(0,4);
②当M在x轴的负半轴、N在y轴的负半轴时,同理可求得M(﹣2,0),N(0,﹣4);
当AB为对角线时,设M(x,0),N(0,y),
∵A(1,6),B(3,2),
∴平行四边形的对称中心为(2,4),
∴x+0=4,y+0=8,解得x=4,y=8,此时M(4,0),N(0,8),
在y=﹣2x+8中,令y=0可得x=4,令x=0可得y=8,
∴A、B、M、N四点共线,不合题意,舍去;
综上可知以M、N、A、B为顶点的四边形是平行四边形时,M(﹣2,0),N(0,﹣4)或M(4,0),N(0,8).

 阅读快车系列答案
阅读快车系列答案