题目内容
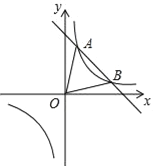
【题目】如图,在平面直角坐标系中,直线y=﹣2x+10与x轴,y轴相交于A,B两点,点C的坐标是(8,4),连接AC,BC.
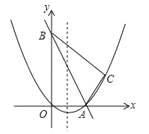
(1)求过O,A,C三点的抛物线的解析式,并判断△ABC的形状;
(2)动点P从点O出发,沿OB以每秒2个单位长度的速度向点B运动;同时,动点Q从点B出发,沿BC以每秒1个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t秒,当t为何值时,PA=QA?
(3)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】(1)![]() ,直角三角形;(2)
,直角三角形;(2)![]() ;(3)M1(
;(3)M1(![]() ,
,![]() ),M2(
),M2(![]() ,
,![]() ),M3(
),M3(![]() ,
,![]() ),M4(
),M4(![]() ,
,![]() ).
).
【解析】
试题分析:(1)先确定出点A,B坐标,再用待定系数法求出抛物线解析式;用勾股定理逆定理判断出△ABC是直角三角形;
(2)根据运动表示出OP=2t,CQ=10﹣t,判断出Rt△AOP≌Rt△ACQ,得到OP=CQ即可;
(3)分三种情况用平面坐标系内,两点间的距离公式计算即可.
试题解析:(1)∵直线y=﹣2x+10与x轴,y轴相交于A,B两点,∴A(5,0),B(0,10),∵抛物线过原点,∴设抛物线解析式为![]() ,∵抛物线过点B(0,10),C(8,4),∴
,∵抛物线过点B(0,10),C(8,4),∴![]() ,∴
,∴ ,∴抛物线解析式为
,∴抛物线解析式为![]() ,∵A(5,0),B(0,10),C(8,4),∴
,∵A(5,0),B(0,10),C(8,4),∴![]() =
=![]() =125,
=125,![]() =
=![]() =100,
=100,![]() =
=![]() =25,∴
=25,∴![]() ,∴△ABC是直角三角形.
,∴△ABC是直角三角形.
(2)如图1,当P,Q运动t秒,即OP=2t,CQ=10﹣t时,由(1)得,AC=OA,∠ACQ=∠AOP=90°,在Rt△AOP和Rt△ACQ中,∵AC=OA,PA=QA,∴Rt△AOP≌Rt△ACQ,∴OP=CQ,∴2t=10﹣t,∴t=![]() ,∴当运动时间为
,∴当运动时间为![]() 时,PA=QA;
时,PA=QA;

(3)存在,∵![]() ,∴抛物线的对称轴为x=
,∴抛物线的对称轴为x=![]() ,∵A(5,0),B(0,10),∴AB=
,∵A(5,0),B(0,10),∴AB=![]()
设点M(![]() ,m);
,m);
①若BM=BA时,∴![]() ,∴m1=
,∴m1=![]() ,m2=
,m2=![]() ,∴M1(
,∴M1(![]() ,
,![]() ),M2(
),M2(![]() ,
,![]() );
);
②若AM=AB时,∴![]() ,∴m3=
,∴m3=![]() ,m4=
,m4=![]() ,∴M3(
,∴M3(![]() ,
,![]() ),M4(
),M4(![]() ,
,![]() );
);
③若MA=MB时,∴![]() ,∴m=5,∴M(
,∴m=5,∴M(![]() ,5),此时点M恰好是线段AB的中点,构不成三角形,舍去;
,5),此时点M恰好是线段AB的中点,构不成三角形,舍去;
∴点M的坐标为:M1(![]() ,
,![]() ),M2(
),M2(![]() ,
,![]() ),M3(
),M3(![]() ,
,![]() ),M4(
),M4(![]() ,
,![]() ).
).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案