题目内容
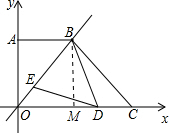
如图,在直角梯形OABC中,AB∥OC,过点O、点B的直线解析式为y=
x,OA、AB是方程x2-14x+48=0的两 个根,OB=BC,D、E分别是线段OC、OB上的动点(点D与点O、点C不重合),且∠BDE=∠ABO,设CD=x,BE=y.
个根,OB=BC,D、E分别是线段OC、OB上的动点(点D与点O、点C不重合),且∠BDE=∠ABO,设CD=x,BE=y.
(1)求BC和OC的长;
(2)求y与x的函数关系式;
(3)是否存在x的值,使以点B、点D、点E为顶点的三角形为等腰三角形?若存在,请直接写出x的值;若不存在,请说明理由.
| 4 |
| 3 |
 个根,OB=BC,D、E分别是线段OC、OB上的动点(点D与点O、点C不重合),且∠BDE=∠ABO,设CD=x,BE=y.
个根,OB=BC,D、E分别是线段OC、OB上的动点(点D与点O、点C不重合),且∠BDE=∠ABO,设CD=x,BE=y.(1)求BC和OC的长;
(2)求y与x的函数关系式;
(3)是否存在x的值,使以点B、点D、点E为顶点的三角形为等腰三角形?若存在,请直接写出x的值;若不存在,请说明理由.
(1)解方程x2-14x+48=0,
得x1=6,x2=8.
过点B作BM⊥OC于点M,
又∵过点O、点B的直线解析式为y=
x,
∴BM:OM=4:3,
∴BM=8,OM=6,
∴BC=OB=
=10,OC=2OM=12;
(2)∵AB∥OC,∴∠ABO=∠BOC,
∵BO=BC,∴∠BOC=∠BCO,
∵∠BDE=∠ABO,∴∠BDE=∠BCO,
∵∠ODB=∠ODE+∠BDE=∠CBD+∠BCO,∴∠ODE=∠CBD,
∴△ODE∽△CBD,∴OD:CB=OE:CD,
∴(12-x):10=(10-y):x,
解得y=
x2-
x+10(0<x<12);
(3)存在x1=2,x2=
,使以点B、点D、点E为顶点的三角形为等腰三角形.理由如下:
∵∠BED>∠BOC=∠BDE,∴BD>BE,
当△BDE为等腰三角形时,分两种情况:
①当DE=DB时,
∵△ODE∽△CBD,
∴OD:CB=DE:BD=1,
∴(12-x):10=1,
解得x=2;
②当EB=ED时,
∵△ODE∽△CBD,
∴OD:CB=OE:CD=DE:BD,
∴(12-x):10=(10-y):x=y:(12-x),
解得x=
.
故存在x1=2,x2=
,使以点B、点D、点E为顶点的三角形为等腰三角形.
得x1=6,x2=8.
过点B作BM⊥OC于点M,
又∵过点O、点B的直线解析式为y=
| 4 |
| 3 |
∴BM:OM=4:3,
∴BM=8,OM=6,
∴BC=OB=
| 62+82 |
(2)∵AB∥OC,∴∠ABO=∠BOC,
∵BO=BC,∴∠BOC=∠BCO,
∵∠BDE=∠ABO,∴∠BDE=∠BCO,
∵∠ODB=∠ODE+∠BDE=∠CBD+∠BCO,∴∠ODE=∠CBD,
∴△ODE∽△CBD,∴OD:CB=OE:CD,
∴(12-x):10=(10-y):x,
解得y=
| 1 |
| 10 |
| 6 |
| 5 |
(3)存在x1=2,x2=
| 11 |
| 3 |
∵∠BED>∠BOC=∠BDE,∴BD>BE,
当△BDE为等腰三角形时,分两种情况:
①当DE=DB时,
∵△ODE∽△CBD,
∴OD:CB=DE:BD=1,
∴(12-x):10=1,
解得x=2;
②当EB=ED时,
∵△ODE∽△CBD,
∴OD:CB=OE:CD=DE:BD,
∴(12-x):10=(10-y):x=y:(12-x),
解得x=
| 11 |
| 3 |
故存在x1=2,x2=
| 11 |
| 3 |


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,过C点作直线CN交x轴于点N,交⊙P于点F,使得△CMN是以MN为底的等腰三角形,经过E、F两点的直线与x轴相交于点Q.
,过C点作直线CN交x轴于点N,交⊙P于点F,使得△CMN是以MN为底的等腰三角形,经过E、F两点的直线与x轴相交于点Q.

 P(0,k)是y轴的负半轴上的一个动点,以P为圆心,3为半径作⊙P.
P(0,k)是y轴的负半轴上的一个动点,以P为圆心,3为半径作⊙P.

