题目内容
如图,在平面直角坐标系中,直线l:y=-2x-8分别与x轴,y轴相交于A,B两点,点 P(0,k)是y轴的负半轴上的一个动点,以P为圆心,3为半径作⊙P.
P(0,k)是y轴的负半轴上的一个动点,以P为圆心,3为半径作⊙P.
(1)连接PA,若PA=PB,试判断⊙P与x轴的位置关系,并说明理由;
(2)当k为何值时,⊙P与直线l相切;
(3)当k为何值时,以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形?
 P(0,k)是y轴的负半轴上的一个动点,以P为圆心,3为半径作⊙P.
P(0,k)是y轴的负半轴上的一个动点,以P为圆心,3为半径作⊙P.(1)连接PA,若PA=PB,试判断⊙P与x轴的位置关系,并说明理由;
(2)当k为何值时,⊙P与直线l相切;
(3)当k为何值时,以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形?
(1)⊙P与x轴相切,
∵直线y=-2x-8与x轴交于A(-4,0),与y轴交于B(0,-8),
∴OA=4,OB=8.
由题意,OP=-k,
∴PB=PA=8+k.
∵在Rt△AOP中,k2+42=(8+k)2
∴k=-3,
∴OP等于⊙P的半径.
∴⊙P与x轴相切.
由y=-2x-8得A(-4,0),B(0,-8),
由勾股定理,得PA=
,
∵PB=k+8,由PA=PB,得
=k+8,
解得k=-3,
∴⊙P与x轴相切;
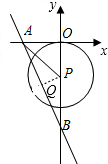 (2)过P点作PQ⊥AB,垂足为Q,由PQ×AB=PB×OA,
(2)过P点作PQ⊥AB,垂足为Q,由PQ×AB=PB×OA,
PQ=
,
P在线段OB上,当⊙P与直线l相切时,PQ=3,即
=3,
解得k=3
-8.
P在线段OB的延长线上,k=-8-(3
-8+8)=-3
-8,⊙P与直线l相切
(3)设⊙P与直线l交于C,D两点,连接PC,PD,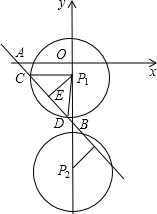
当圆心P1在线段OB上时,作P1E⊥CD于E,
∵△P1CD为正三角形,
∴DE=
CD=
,P1D=3.
∴P1E=
.
∵∠AOB=∠P1EB=90°,∠ABO=∠P1BE,
∴△AOB∽△P1EB.
∴
=
,即
=
,
∴P1B=
,(2分)
∴P1O=BO-BP1=8-
.
∴P1(0,
-8).
∴k=
-8.(2分)
当圆心P2在线段OB延长线上时,
∵P2B=
,
∴P2O=BO+BP2=
+8.
∴P2(0,-
-8).
∴k=-
-8.(2分)
∴当k=
-8或k=-
-8时,以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形.
∵直线y=-2x-8与x轴交于A(-4,0),与y轴交于B(0,-8),
∴OA=4,OB=8.
由题意,OP=-k,
∴PB=PA=8+k.
∵在Rt△AOP中,k2+42=(8+k)2
∴k=-3,
∴OP等于⊙P的半径.
∴⊙P与x轴相切.
由y=-2x-8得A(-4,0),B(0,-8),
由勾股定理,得PA=
| 16+k2 |
∵PB=k+8,由PA=PB,得
| 16+k2 |
解得k=-3,
∴⊙P与x轴相切;
 (2)过P点作PQ⊥AB,垂足为Q,由PQ×AB=PB×OA,
(2)过P点作PQ⊥AB,垂足为Q,由PQ×AB=PB×OA,PQ=
| (k+8)×4 | ||
|
P在线段OB上,当⊙P与直线l相切时,PQ=3,即
| (k+8)×4 | ||
|
解得k=3
| 5 |
P在线段OB的延长线上,k=-8-(3
| 5 |
| 5 |
(3)设⊙P与直线l交于C,D两点,连接PC,PD,

当圆心P1在线段OB上时,作P1E⊥CD于E,
∵△P1CD为正三角形,
∴DE=
| 1 |
| 2 |
| 3 |
| 2 |
∴P1E=
3
| ||
| 2 |
∵∠AOB=∠P1EB=90°,∠ABO=∠P1BE,
∴△AOB∽△P1EB.
∴
| AO |
| AB |
| P1E |
| P1B |
| 4 | ||
4
|
| ||||
| P1B |
∴P1B=
3
| ||
| 2 |
∴P1O=BO-BP1=8-
3
| ||
| 2 |
∴P1(0,
3
| ||
| 2 |
∴k=
3
| ||
| 2 |
当圆心P2在线段OB延长线上时,
∵P2B=
3
| ||
| 2 |
∴P2O=BO+BP2=
3
| ||
| 2 |
∴P2(0,-
3
| ||
| 2 |
∴k=-
3
| ||
| 2 |
∴当k=
3
| ||
| 2 |
3
| ||
| 2 |

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 个根,OB=BC,D、E分别是线段OC、OB上的动点(点D与点O、点C不重合),且∠BDE=∠ABO,设CD=x,BE=y.
个根,OB=BC,D、E分别是线段OC、OB上的动点(点D与点O、点C不重合),且∠BDE=∠ABO,设CD=x,BE=y.


 交于Q点(如图所示),若四边形PQOB的面积是
交于Q点(如图所示),若四边形PQOB的面积是

 交行李托运费.行李费托运费y(元)与行李重量x(千克)之间的函数关系如图所示.
交行李托运费.行李费托运费y(元)与行李重量x(千克)之间的函数关系如图所示.