Question

在△ABC中，点D、E分别在边AB、AC上，BD=2AD，CE=2AE，

BC

=

a

，那么

ED

等于（　　）

• A、

  1

  3

  a

• B、-

  1

  3

  a

• C、

  1

  2

  a

• D、-

  1

  2

  a

Answer 1

分析：在△ABC中，点D、E分别在边AB、AC上，BD=2AD，CE=2AE，故DE=

1

3

BC，再根据平面向量的定义，既有方向，又有大小，即可得出答案．

解答：解：根据题意画出图形如下所示：

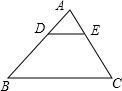
∵在△ABC中，点D、E分别在边AB、AC上，BD=2AD，CE=2AE，
∴ED=

1

3

BC，
又

ED

与

BC

反向，
∴

ED

=-

1

3

BC

．
故选B．

点评：本题考查了平面向量的知识，属于基础题，比较简单，注意熟练掌握平面向量的概念是关键．