题目内容
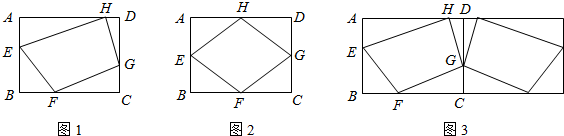
(2012•西城区一模)如图,在△ABC中,点D是BC上一点,∠B=∠DAC=45°.
(1)如图1,当∠C=45°时,请写出图中一对相等的线段;
(2)如图2,若BD=2,BA=
,求AD的长及△ACD的面积.

(1)如图1,当∠C=45°时,请写出图中一对相等的线段;
AB=AC或AD=BD=CD;
AB=AC或AD=BD=CD;
.(2)如图2,若BD=2,BA=
| 3 |

分析:(1)由∠C=45°,∠B=∠DAC=45°,易得△ABD,△ACD,△ABC是等腰直角三角形,继而求得答案;
(2)首先过点A作AE⊥BC于E,由直角三角形的性质,可求得AD的长,又由△ADC∽△BAC,即可利用相似三角形的面积比等于相似比的平方,求得△ACD的面积.
(2)首先过点A作AE⊥BC于E,由直角三角形的性质,可求得AD的长,又由△ADC∽△BAC,即可利用相似三角形的面积比等于相似比的平方,求得△ACD的面积.
解答:解:(1)∵∠C=45°,∠B=∠DAC=45°,
∴∠BAC=∠ADC=∠ADB=90°,
∴∠BAD=∠CAD=∠B=∠C=45°,
∴AB=AC或AD=BD=CD;
故答案为:AB=AC或AD=BD=CD;
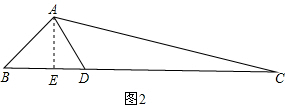 (2)过点A作AE⊥BC于E,
(2)过点A作AE⊥BC于E,
∵∠B=45°,BA=
,
∴AE=BE=
=
,
∵BD=2,
∴DE=2-
,
在Rt△ADE中,AD=
=
=
=
-1;
∵∠B=∠DAC=45°,∠C是公共角,
∴△ADC∽△BAC,
∴
=(
)2,
∵S△ABD=
BD•AE=
×2×
,
设S△ADC=x,
则
=(
)2,
∴S△ACD=
.
∴AD=
-1;S△ACD=
.
∴∠BAC=∠ADC=∠ADB=90°,
∴∠BAD=∠CAD=∠B=∠C=45°,
∴AB=AC或AD=BD=CD;
故答案为:AB=AC或AD=BD=CD;
 (2)过点A作AE⊥BC于E,
(2)过点A作AE⊥BC于E,∵∠B=45°,BA=
| 3 |
∴AE=BE=
| AB | ||
|
| ||
| 2 |
∵BD=2,
∴DE=2-
| ||
| 2 |
在Rt△ADE中,AD=
| AE2+DE2 |
7-2
|
(
|
| 6 |
∵∠B=∠DAC=45°,∠C是公共角,
∴△ADC∽△BAC,
∴
| S△ADC |
| S△ABC |
| AD |
| AB |
∵S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
设S△ADC=x,
则
| x | ||||
x+
|
| ||
|
∴S△ACD=
9+
| ||
| 4 |
∴AD=
| 6 |
9+
| ||
| 4 |
点评:此题考查了相似三角形的判定与性质、勾股定理、等腰直角三角形的性质.此题难度较大,注意掌握辅助线的作法是解此题的关键,注意数形结合思想与方程思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目