题目内容
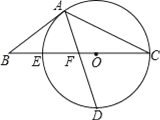
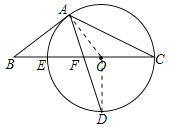
【题目】如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF.
(1)求证:AB是⊙O的切线;
(2)若CF=4,DF=![]() ,求⊙O的半径r及sinB.
,求⊙O的半径r及sinB.
【答案】(1)证明见解析;(2)r=3,sinB=![]() .
.
【解析】试题分析:(1)连接OA、OD,如图,根据垂径定理得OD⊥BC,则∠D+∠OFD=90°,再由AB=BF,OA=OD得到∠BAF=∠BFA,∠OAD=∠D,加上∠BFA=∠OFD,所以∠OAD+∠BAF=90°,则OA⊥AB,然后根据切线的判定定理即可得到AB是⊙O切线;
(2)先表示出OF=4﹣r,OD=r,在Rt△DOF中利用勾股定理建立方程,解方程得到r的值,那么OA=3,OF=CF﹣OC=4﹣3=1,BO=BF+FO=AB+1.
然后在Rt△AOB中利用勾股定理,得到AB的值,再根据三角函数定义求出sinB.
试题解析:(1)证明:连接OA、OD,如图,∵点D为CE的下半圆弧的中点,∴OD⊥BC,∴∠EOD=90°,∵AB=BF,OA=OD,∴∠BAF=∠BFA,∠OAD=∠D,而∠BFA=∠OFD,∴∠OAD+∠BAF=∠D+∠BFA=90°,即∠OAB=90°,∴OA⊥AB,∴AB是⊙O切线;
(2)解:OF=CF﹣OC=4﹣r,OD=r,DF=![]() ,在Rt△DOF中,
,在Rt△DOF中, ![]() ,即
,即![]() ,解得:r=3或r=1(舍去);∴半径r=3,∴OA=3,OF=CF﹣OC=4﹣3=1,BO=BF+FO=AB+1.在Rt△AOB中,
,解得:r=3或r=1(舍去);∴半径r=3,∴OA=3,OF=CF﹣OC=4﹣3=1,BO=BF+FO=AB+1.在Rt△AOB中, ![]() ,∴
,∴![]() ,∴AB=4,OB=5,∴sinB=
,∴AB=4,OB=5,∴sinB=![]() =
=![]() .
.

练习册系列答案
相关题目