题目内容
【题目】如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连结EF.若EF=2 ![]() ,BD=8,则菱形ABCD的周长为( )
,BD=8,则菱形ABCD的周长为( ) 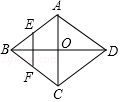
A.8
B.8 ![]()
C.16 ![]()
D.8 ![]()
【答案】D
【解析】解:∵E,F分别是AB,BC边上的中点,EF=2 ![]() , ∴AC=2EF=4
, ∴AC=2EF=4 ![]() ,
,
∵四边形ABCD是菱形,
∴AC⊥BD,OA= ![]() AC=2
AC=2 ![]() ,OB=
,OB= ![]() BD=4,
BD=4,
∴AB= ![]() =2
=2 ![]() ,
,
∴菱形ABCD的周长为8 ![]() .
.
故选:D.
【考点精析】通过灵活运用三角形中位线定理和菱形的性质,掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半即可以解答此题.

练习册系列答案
相关题目
【题目】1~6个月的婴儿生长发育得非常快,出生体重为4000克的婴儿,他们的体重y(克)和月龄x(月)之间的关系如下表:
月龄/(月) | 1 | 2 | 3 | 4 | 5 |
体重/(克) | 4700 | 5400 | 6100 | 6800 | 7500 |
则6个月大的婴儿的体重约为________.