题目内容
已知m2+2mn+2n2-6n+9=0,求
的值.
解:∵m2+2mn+2n2-6n+9=0
∴(m+n)2+(n-3)2=0
∴(m+n)2=0,(n-3)2=0
∴n=3,m=-3
∴
=
=-
根据你的观察,探究下面的问题:
(1)已知x2+4x+4+y2-8y+16=0,求
的值;
(2)已知a,b,c是△ABC的三边长,且满足a2+b2-8b-10a+41=0,求△ABC中最大边c的取值范围;
(3)试说明不论x,y取什么有理数时,多项式x2+y2-2x+2y+3的值总是正数.
| m |
| n2 |
解:∵m2+2mn+2n2-6n+9=0
∴(m+n)2+(n-3)2=0
∴(m+n)2=0,(n-3)2=0
∴n=3,m=-3
∴
| m |
| n2 |
| -3 |
| 9 |
| 1 |
| 3 |
根据你的观察,探究下面的问题:
(1)已知x2+4x+4+y2-8y+16=0,求
| y |
| x |
(2)已知a,b,c是△ABC的三边长,且满足a2+b2-8b-10a+41=0,求△ABC中最大边c的取值范围;
(3)试说明不论x,y取什么有理数时,多项式x2+y2-2x+2y+3的值总是正数.
分析:(1)按照题目提供的方法将x2+4x+4+y2-8y+16=0配方后即可求得x、y的值即可求解;
(2)求得三角形的两边后即可求得第三边的取值范围;
(3)将其整理成完全平方数加正数的形式即可证得结论.
(2)求得三角形的两边后即可求得第三边的取值范围;
(3)将其整理成完全平方数加正数的形式即可证得结论.
解答:解:(1)∵x2+4x+4+y2-8y+16=0
∴(x+2)2+(y-4)2=0,
∴(x+2)2=0,(y-4)2=0,
∴x=-2,y=4
∴
=-
;
(2))∵a2+b2-8b-10a+41=0,
∴(a-5)2+(b-4)2=0,
∴(a-5)2=0,(b-4)2=0,
∴a=5,b=4
△ABC中最大边5<c<9;
(3))∵x2+y2-2x+2y+3=(x-1)2+(y+1)2+1,
且(x-1)2≥0,(y+1)2≥0,
∴x=-2,y=4
∴(x-1)2+(y+1)2+1>0,
∴多项式x2+y2-2x+2y+3的值总是正数.
∴(x+2)2+(y-4)2=0,
∴(x+2)2=0,(y-4)2=0,
∴x=-2,y=4
∴
| y |
| x |
| 1 |
| 2 |
(2))∵a2+b2-8b-10a+41=0,
∴(a-5)2+(b-4)2=0,
∴(a-5)2=0,(b-4)2=0,
∴a=5,b=4
△ABC中最大边5<c<9;
(3))∵x2+y2-2x+2y+3=(x-1)2+(y+1)2+1,
且(x-1)2≥0,(y+1)2≥0,
∴x=-2,y=4
∴(x-1)2+(y+1)2+1>0,
∴多项式x2+y2-2x+2y+3的值总是正数.
点评:本题考查了配方法的应用,特别是判断一个算式是正数时总是将其整理成一个完全平方公式加正数的形式.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
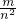 的值.
的值.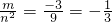
 的值;
的值;