题目内容
(1)已知关于x的不等式ax+1>0(其中a≠0)①当a=-2时,求此不等式的解,并在数轴上表示此不等式的解集;
②小明准备了十张形状、大小完全相同的不透明的卡片,上面分别写有整数-10、-9、-8、-7、-6、-5、-4、-3、-2、-1,将这10张卡片写有整数的一面向下放在桌面上,从中任意抽取一张,以卡片上的数作为不等式的系数a,求使该不等式没有正整数解的概率;
(2)若关于x的不等式ax+b>0(其中a≠0)a 的与(1)②相同,且使该不等式有正整数解的概率为
| 1 | 2 |
分析:(1)①根据是不等式的解法,当a=-2时,求出不等式的解,并在数轴上表示此不等式的解集即可;
②根据a的值为:-10、-9、-8、-7、-6、-5、-4、-3,-2,-1,分别求出即可;
(2)只需求出相应的一元一次不等式的解集,利用概率的意义便可解决问题.
②根据a的值为:-10、-9、-8、-7、-6、-5、-4、-3,-2,-1,分别求出即可;
(2)只需求出相应的一元一次不等式的解集,利用概率的意义便可解决问题.
解答:解:(1)①当a=-2时,
∴-2x+1>0,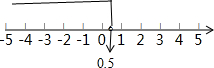
∴-2x>-1,
∴x<0.5
②由ax+1>0可得:x<-
,
要使ax+1>0无正整数解,则-
<1,
所以a的值为:-10、-9、-8、-7、-6、-5、-4、-3,-2,-1,
取a=-1,不等式ax+1>0的解为x<1,不等式没有正整数解.
取a=-2,不等式ax+1>0的解为x<
,不等式没有正整数解.
取a=-3,不等式ax+1>0的解为x<
,不等多没有正整数解.
取a=-4,不等式ax+1>0的解为x<
,不等式没有正整数解.
…
∴整数a取-1至-10中任意一个整数时,不等式没有正整数解.
P(不等式没有正整数解)=1.
(2)∵若关于x的不等式ax+b>0(其中a≠0)a 的与(1)②相同,
∴ax>-b,
x<-
,
∴当b=6时,
∵取a=-1,不等式ax+b>0的解为x<b,∴x<6,不等式有正整数解.
取a=-2,不等式ax+b>0的解为x<
,∴x<3,不等式有正整数解.
取a=-3,不等式ax+b>0的解为x<
,∴x<2,不等式有正整数解.
取a=-4,不等式ax+b>0的解为x<
,∴x<1.5,不等式有正整数解.
取a=-5,不等式ax+b>0的解为x<
,∴x<1.2,不等式有正整数解.
取a=-6,不等式ax+b>0的解为x<
,∴x<1,不等式没有正整数解.
…
∴整数a取-1至-10中任意一个整数时,要使该不等式有正整数解的概率为
,
∴当<b≤6时,
不等式有正整数解的概率为
.
∴-2x+1>0,
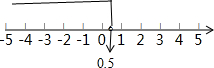
∴-2x>-1,
∴x<0.5
②由ax+1>0可得:x<-
| 1 |
| a |
要使ax+1>0无正整数解,则-
| 1 |
| a |
所以a的值为:-10、-9、-8、-7、-6、-5、-4、-3,-2,-1,
取a=-1,不等式ax+1>0的解为x<1,不等式没有正整数解.
取a=-2,不等式ax+1>0的解为x<
| 1 |
| 2 |
取a=-3,不等式ax+1>0的解为x<
| 1 |
| 3 |
取a=-4,不等式ax+1>0的解为x<
| 1 |
| 4 |
…
∴整数a取-1至-10中任意一个整数时,不等式没有正整数解.
P(不等式没有正整数解)=1.
(2)∵若关于x的不等式ax+b>0(其中a≠0)a 的与(1)②相同,
∴ax>-b,
x<-
| b |
| a |
∴当b=6时,
∵取a=-1,不等式ax+b>0的解为x<b,∴x<6,不等式有正整数解.
取a=-2,不等式ax+b>0的解为x<
| b |
| 2 |
取a=-3,不等式ax+b>0的解为x<
| b |
| 3 |
取a=-4,不等式ax+b>0的解为x<
| b |
| 4 |
取a=-5,不等式ax+b>0的解为x<
| b |
| 5 |
取a=-6,不等式ax+b>0的解为x<
| b |
| 6 |
…
∴整数a取-1至-10中任意一个整数时,要使该不等式有正整数解的概率为
| 1 |
| 2 |
∴当<b≤6时,
不等式有正整数解的概率为
| 1 |
| 2 |
点评:此题主要考查了不等式与概率的简单应用,只需求出相应的一元一次不等式的解集,利用概率的意义便可解决问题.

练习册系列答案
相关题目
已知关于x的方程(m+2)x2-3x+1=0有两个不相等的实数根,则m的取值范围是( )
A、m<
| ||
B、m<-
| ||
C、m<
| ||
D、m<-
|