题目内容
如图,PA、PB是⊙O的切线,A、B为切点,连接OA、OB、AB,若∠P=60°,则∠OAB= ____ . 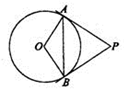

30
只要根据切线的性质找出∠OAP=∠OBP=90°,再根据四边形的内角和定理即可解.
解:PA,PB是⊙O的切线,A,B为切点,
∴∠OAP=∠OBP=90°,∠AOB=180°-∠P=120°,
∵AO=OB,
∴∠OAB=∠OBA=(180°-∠AOB)÷2=30°.
故答案为:30°.
解:PA,PB是⊙O的切线,A,B为切点,
∴∠OAP=∠OBP=90°,∠AOB=180°-∠P=120°,
∵AO=OB,
∴∠OAB=∠OBA=(180°-∠AOB)÷2=30°.
故答案为:30°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 上,AF⊥ED,交ED的延长线与点F,如果正方形的边长为1,则图中阴影部分的面积是__________.
上,AF⊥ED,交ED的延长线与点F,如果正方形的边长为1,则图中阴影部分的面积是__________.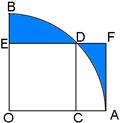
 ;
;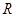 的长为
的长为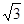 cm,用它围成一个圆锥的侧面(接缝忽略不计),则该圆锥的侧面积为
cm,用它围成一个圆锥的侧面(接缝忽略不计),则该圆锥的侧面积为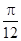
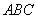 的一腰
的一腰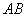 为直径的⊙O交底边
为直径的⊙O交底边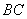 于点
于点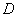 ,交
,交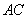 于点
于点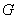 ,连结
,连结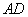 ,并过点
,并过点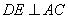 ,垂足为
,垂足为 .根据以上条件写出三个正确结论(除
.根据以上条件写出三个正确结论(除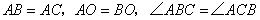 外)是:
外)是: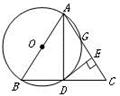
 ,则sin
,则sin