题目内容
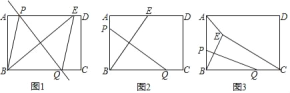
【题目】如图，将一个等腰直角三角形按图中方式依次翻折，若DE=a，DC=b，则下列说法：①DC′平分∠BDE；②BC的长为2a+b；③△BC′D是等腰三角形；④△CED的周长等于BC的长.其中正确的是（）
A.①②③B.②④C.②③④D.③④
【答案】C
【解析】
根据折叠前后计算得到∠BDC′=22.5°，∠C′DE=45°，可判断①；
根据折叠的性质知，BE=AB=AC=a+b,EC=DE=b,由此可表示出BC的长，可判断②；
分别表示出BC′和DC′的长，可判断③；
表示出△CED的周长=CE+DE+CD= a+b+a=2a+b，可判断④.
解：∵∠BDC′=22.5°，∠C′DE=45°，
∴①错误；
根据折叠的性质知，BE=AB=AC=a+b,EC=DE=b,
∴BC=BE+EC=a+b+a=2a+b，
∴②正确；
∵△C′ED≌△CED，且都是等腰直角三角形，
∴C′D=CD=b，C′E=CE=a,
∴BC′=BE- C′E=a+b-a=b，
∴BC′=DC′，
∴△BC′D是等腰三角形；
故③正确；
∵△CED的周长=CE+DE+CD= a+b+a=2a+b =BC，
故④正确．
故选：C．
练习册系列答案
阅读快车系列答案
相关题目
