题目内容
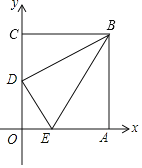
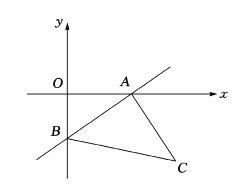
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 相交于点
相交于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)在![]() 轴上一点
轴上一点![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)直线![]() 上一点
上一点![]() ,平面内一点
,平面内一点![]() ,若以
,若以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等,求点
全等,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)点
;(2)点![]() 坐标为
坐标为![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)令![]() 中y=0即可求得答案;
中y=0即可求得答案;
(2)点![]() 在
在![]() 的下方,过点D作DE∥AC交y轴于E,求出DE的解析式即可得到点E的坐标,利用对称性即可得到点E在AC上方时点E的坐标;
的下方,过点D作DE∥AC交y轴于E,求出DE的解析式即可得到点E的坐标,利用对称性即可得到点E在AC上方时点E的坐标;
(3)求出直线与x轴的夹角度数,线段AD的长度,分三种情况求出点F的坐标.
(1)∵点![]() 是
是![]() 与
与![]() 轴的交点,
轴的交点,![]() 代入
代入![]() ,
,![]() ,
,
∴点![]() 的坐标
的坐标![]() ;
;
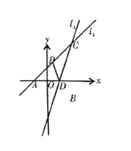
(2)当点![]() 在
在![]() 的下方,过点
的下方,过点![]() 作
作![]() ,交
,交![]() 轴于点
轴于点![]() ,
,
设![]() 解析式为
解析式为![]() ,过
,过![]() ,
,
∴2+b=0,得b=-2,
∴![]() ,
,
∴![]() ,
,
点![]() 在
在![]() 上方,同理可得
上方,同理可得![]() ,
,
综上:点![]() 坐标为
坐标为![]() 或
或![]()
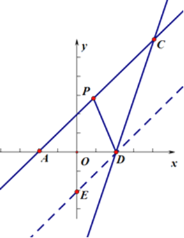
(3)直线![]() 与x轴的夹角是45
与x轴的夹角是45![]() ,
,
∵A(-2,0),D(2,0),
∴AD=4,
作AF1⊥x轴,当A1F=AD=4时,△AF1P≌△ADP,此时点F1的坐标是(-2,4);
作PF2∥AD,当F2=AD=4时,△APF2≌△PAD,此时点F2的坐标是(-3,3);
作PF3⊥x轴,当PF3=AD=4时,△APF3≌△PAD,此时点F3的坐标是(1,-1),
综上,点F的坐标为 ![]() .
.

练习册系列答案
相关题目