Question

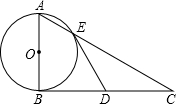
AB为⊙O的直径，C为⊙O上一点，AD和过C点的切线相交于D，和⊙O相交于E．如果AC平分∠DAB，
（1）求证：∠ADC=90°；
（2）若AB=2r，AD=

8

5

r，求DE．

Answer 1

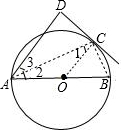
（1）证明：连接OC，
∵CD是⊙O的切线，
∴OC⊥CD，（1分）
∵OA=OC，
∴∠1=∠2，
∵∠2=∠3，∴∠1=∠3，
∴AD∥OC，（2分）
∴AD⊥CD，
即∠ADC=90°．（3分）

（2）连接BC，则∠ACB=90°，（4分）
由（1）得∠2=∠3，∠ACB=∠ADC=90°，
∴Rt△ABC∽Rt△ACD，
∴

AC

AD

=

AB

AC

，（5分）
即AC²=AB•AD=2r•

8

5

r=

16

5

r2，
又∵CD²=AC²-AD²=

16

5

r2-

64

25

r2=

16

25

r2，
且CD²=DE•AD，
∴DE=

CD2

AD

=

16 25 r2

8 5 r

=

2

5

r．（7分）