题目内容
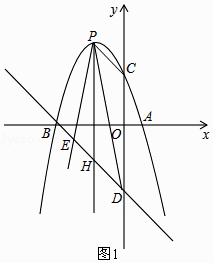
【题目】如图，在平面直角坐标系中，O为坐标原点，抛物线y=﹣x2+bx+3与x轴交于点A（1，0）和点B，与y轴交于点C．
（1）求抛物线的解析式．
（2）直线y=kx+3k经过点B，与y轴的负半轴交于点D，点P为第二象限内抛物线上一点，连接PD，射线PD绕点P顺时针旋转与线段BD交于点E，且∠EPD=2∠PDC，∠EPD的平分线交线段BD于点H，∠BEP+∠BDP=90°
①若四边形PHDC是平行四边形，求点P的坐标；
②过点E作EF⊥PD，交PD于点G，交y轴于点F，已知PF=3 
，求直线PF的解析式．
【答案】
（1）
解：把A（1，0）代入y=﹣x2+bx+3中，
﹣1+b+3=0，解得：b=﹣2，
∴抛物线的解析式为：y=﹣x2﹣2x+3；
（2）
解：如图1，当y=0时，﹣x2﹣2x+3=0，
x2+2x﹣3=0，
（x+3）（x﹣1）=0，
x1=﹣3，x2=1，
∴B（﹣3，0），
∵四边形PHDC是平行四边形，
∴PH∥DC，
∴∠EHP=∠EDC，∠HPD=∠PDC，
设∠PDC=x，∠BDP=y，则∠EPH=∠HPD=x，∠EHP=∠EDC=x+y，
∴∠BEP=∠BHP+∠EPH=x+y+x=2x+y，
∵∠BEP+∠BDP=90°，
∴2x+y+y=90°，
x+y=45°，
即∠BHP=45°，
∴∠BDC=45°，
∴△BOD是等腰直角三角形，
∴OB=OD=3=﹣3k，
k=﹣1，
∴直线BD的解析式为：y=﹣x﹣3，
∵PH⊥x轴，
设P（x，﹣x2﹣2x+3），H（x，﹣x﹣3），
∴PH=CD=6，
∴﹣x2﹣2x+3+x+3=6，
解得：x1=0（舍），x2=﹣1，
∴P（﹣1，4）；
②如图2，过D作DQ⊥y轴交PE的延长线于Q，直线PH交DQ于M，PN⊥y轴于N，
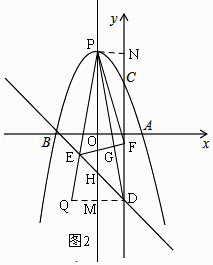
∵∠PDC= 
∠EPD=∠DPH，
∴PM∥DN，
∵DQ⊥DN，
而PM平分∠QPD，
∴MQ=MD，
易得四边形PNDM为矩形，
∴MD=PN，
∴DQ=2PN，
∵EF⊥PD，
∴∠BDP+∠DEG=90°，
而∠BDP+∠BEP=90°，
∴∠DEG=∠BEP=∠QED，
∵∠BDF=45°，
∴∠QDE=45°，
在△DEQ和△DEF中，
，
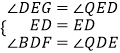∴△DEQ≌△DEF（ASA），
∴DQ=DF，
∴DF=2MD=2PN，
设P（x，﹣x2﹣2x+3），则PN=DM=﹣x，DF=﹣2x，FN=﹣x2﹣2x+3+3+2x=﹣x2+6，
在Rt△PFN中，由勾股定理得：PF2=PN2+FN2，
∴ 
=（﹣x）2+（﹣x2+6）2，
解得：x1= 
，x2=±3，
∵点P为第二象限内抛物线上一点，
∴x=﹣ 
，
∴DF=2 ，
∴P（﹣ ，2 ﹣3），F（0，2 ﹣3），
设PF解析式为：y=kx+b，
把P（﹣ ，2 ﹣3），F（0，2 ﹣3）代入得：
，
∴ 
，
∴直线PF的解析式为：y=﹣2 x+2 ﹣3．
【解析】（1）把点A的坐标代入抛物线的解析式中可得结论；（2）①如图1，推出∠BHP=45°，求出直线BD解析式：y=﹣x﹣3，求出P点坐标等于（﹣1，4）；②如图2，作辅助线，构建矩形和等腰三角形，判断四边形PNDM为矩形得到MD=PN，则DQ=2PN，然后证明△DEQ≌△DEF得到DQ=DF，所以DF=2MD=2PN；再在Rt△PFN中利用勾股定理列方程得出P和F的坐标，根据待定系数法求直线PF的解析式．
【考点精析】认真审题，首先需要了解二次函数的性质(增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小)，还要掌握等腰三角形的性质(等腰三角形的两个底角相等（简称：等边对等角）)的相关知识才是答题的关键．
