��Ŀ����
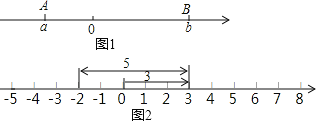
����Ŀ���Ķ����ϣ���ͼ1��ʾ����A��B�������Ϸֱ��ʾ������a��b��A��B����֮��ľ����ʾΪAB����������A��B����֮��ľ���AB=|a��b|�����磺|5������2��|��ʾ5�멁2֮��ľ���ֵ��ʵ����Ҳ������Ϊ5�멁2����������������Ӧ������֮��ľ��룮
��1����ͼ2��ʾ��һ����������ϵ�ԭ�㿪ʼ���������ƶ�3����λ���ȣ��������ƶ�5����λ���ȣ����Կ����յ��ʾ�����ǩ�2���������ν��˼�룬�������ͼ��˼����������и��⣺
�������ϱ�ʾ2�멁5������֮��ľ������� ������λ���ȣ�
���������ϵĵ�A��ʾ����Ϊx����B��ʾ����Ϊ��1����A��B����ľ�����Ա�ʾΪ�� ������|x+1|=3����xΪ�� ����
�������A��ʾ����1����A�������ƶ�18����λ���ȣ��������ƶ�13����λ�����յ�ΪB����ôA��B�����ľ������� ����
��2���������ϵĵ�A��ʾ����Ϊx��xΪ��������xΪ�� ��ʱ��|x+5|��|x��7|��ֵ��ȣ�
���𰸡���1����7����|x+1|��-4��2����5����2��x=1
��������
��1���ٸ��������ľ��빫ʽ������⣻
�ڸ��������ľ��빫ʽ����A��B����ľ��룻���ݾ���ֵ�����ʵõ�x+1=��3���ⷽ�̼�����⣻
���ȸ�������Ҽ������B��ʾ�������ٸ��������ľ��빫ʽ������⣻
��2����������ɵ�|x+5|=|x-7|���ⷽ�̼�����⣮
�⣺��1���������ϱ�ʾ2��-5������֮��ľ�����2-��-5��=7����λ���ȣ�
�ʴ�Ϊ��7��
���������ϵĵ�A��ʾ����Ϊx����B��ʾ����Ϊ-1����A��B����ľ�����Ա�ʾΪ|x+1|��
|x+1|=3��
x+1=��3��
���x=-4��2��
�ʴ�Ϊ��|x+1|��-4��2��
��B���ʾ������-1+18-13=4��
��A��B�����ľ�����4-��-1��=5��
�ʴ�Ϊ�� 5��
��2����������|x+5|=|x-7|��
x+5=x-7��x+5=-��x-7����
��x+5=x-7ʱ�������⣻
��x+5=-��x-7��ʱ�����x=1��
�ʵ�xΪ1ʱ��|x+5|��|x-7|��ֵ��ȣ�

����Ŀ��ij���������A ����������ӻ��ְ����£�
���� | �������� | ʤ�� | ���� | ���� |
��һ˫¹ | 20 | 18 | 2 | 38 |
������ | 20 | 14 | 6 | 34 |
�㽭���� | 20 | 7 | 13 | 27 |
����ʨ | 20 | 0 | 20 | 20 |
��1���ñ���ʤ1���Ļ���Ϊ �֣���1���Ļ���Ϊ �֣� ��ʽ��ʾ������ʤ��������֮���������ϵ������ʤ����Ϊm��������α����Ļ����� ��ֱ��д�������
��2��ij�ӵ�ʤ���ܻ����ܵ������ĸ����ܻ�����
����Ŀ��Ϊ������Ӧ�����ﴫͳ�Ļ����ĺ��٣�ijѧУ����ȫУ1200��ѧ�����о���ʫ���б�������ڻ֮��ٰ쾭��ʫ�ʴ�����Ϊ�˽Ȿ��ϵ�л�ij���Ч����ѧУ��ί�ڻ����֮���������ȡ����ѧ��������һ��ʫ���б��������������������Ƴɵ�ͳ��ͼ�����֣���ͼ��ʾ��
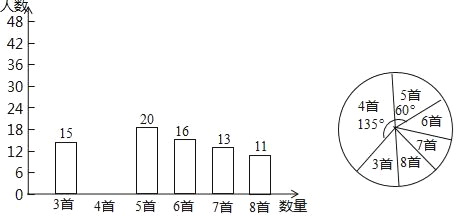
����������һ���£��ٴγ���ⲿ��ѧ����һ��ʫ���б������������Ƴ�ͳ�Ʊ�
һ��ʫ���б����� | 3�� | 4�� | 5�� | 6�� | 7�� | 8�� |
���� | 10 | 10 | 15 | 40 | 25 | 20 |
����ݵ������Ϣ
��1�������֮��ѧ����һ��ʫ���б�����������λ��Ϊ������
��2�����ƴ�����һ���¸�Уѧ��һ��ʫ���б�6�ף���6�ף����ϵ�������
��3��ѡ���ʵ���ͳ��������������ͬ�ĽǶȷ������ε����������ݣ����۸�У����ʫ���б�ϵ�л��Ч����
����Ŀ���ɾ����ù㳡��![]() ��
��![]() ��
��![]() �տ�ҵ���̳������ҷ�װ����п�ҵ��������������ҷ�װ���Żݻ���±���
�տ�ҵ���̳������ҷ�װ����п�ҵ��������������ҷ�װ���Żݻ���±���
�����װ�ܽ�Ԫ�� | ������ | ���� |
|
�Żݷ��� | �� | �� | �� |
�ҷ�װ���Żݻ�������װ�ܽ��ÿ��![]() Ԫ��
Ԫ��![]() Ԫ.
Ԫ.
���磺�����ܽ����![]() Ԫ��
Ԫ��![]() Ԫ����
Ԫ����![]() Ԫ��
Ԫ��![]() Ԫ���Դ�����.
Ԫ���Դ�����.
��1���������ҵ깺���װ�ܽ���![]() Ԫ���ļҵ�ʵ�ʸ�����٣��ٶ��٣�
Ԫ���ļҵ�ʵ�ʸ�����٣��ٶ��٣�
��2���������װ�ܽ��С��![]() Ԫ��ѡ���ļҵ깺���װ�����㣿��ͨ������˵������.
Ԫ��ѡ���ļҵ깺���װ�����㣿��ͨ������˵������.

