题目内容
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转得到
顺时针旋转得到![]() ,点
,点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,若点
的中点,若点![]() 刚好落在边
刚好落在边![]() 上,则
上,则![]() ______.
______.
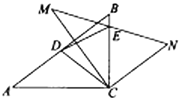
【答案】![]()
【解析】
根据旋转性质及直角三角形斜边中线等于斜边一半,求出CD=CE=5,再根据勾股定理求DE长,![]() 的值即为等腰△CDE底角的正弦值,根据等腰三角形三线合一构建直角三角形求解.
的值即为等腰△CDE底角的正弦值,根据等腰三角形三线合一构建直角三角形求解.
如图,过D点作DM⊥BC,垂足为M,过C作CN⊥DE,垂足为N,
在Rt△ACB中,AC=8,BC=6,由勾股定理得,AB=10,
∵D为AB的中点,
∴CD=![]() ,
,
由旋转可得,∠MCN=90°,MN=10,
∵E为MN的中点,
∴CE=![]() ,
,
∵DM⊥BC,DC=DB,
∴CM=BM=![]() ,
,
∴EM=CE-CM=5-3=2,
∵DM=![]() ,
,
∴由勾股定理得,DE=![]() ,
,
∵CD=CE=5,CN⊥DE,
∴DN=EN=![]() ,
,
∴由勾股定理得,CN=![]() ,
,
∴sin∠DEC=![]() .
.

故答案为:![]() .
.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
【题目】为了掌握八年级数学考试卷的命题质量与难度系数,命题组教师赴外地选取一个水平相当的八年级班级进行预测,将考试成绩分布情况进行处理分析,制成频数分布表如下(成绩得分均为整数):
组别 | 成绩分组 | 频数频率 | 频数 |
1 |
| 2 | 0.05 |
2 |
| 4 | 0.10 |
3 |
|
| 0.2 |
4 |
| 10 | 0.25 |
5 |
|
|
|
6 |
| 6 | 0.15 |
合计 | 40 | 1.00 |
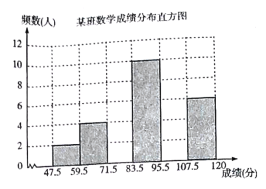
根据表中提供的信息解答下列问题:
(1)频数分布表中的![]() ,
,![]() ,
,![]() ;
;
(2)已知全区八年级共有200个班(平均每班40人),用这份试卷检测,108分及以上为优秀,预计优秀的人数约为 ,72分及以上为及格,预计及格的人数约为 ,及格的百分比约为 ;
(3)补充完整频数分布直方图.