题目内容
 已知:在Rt△ABC中,∠ABC=90°,以直角边AB为直径作⊙O,⊙O与斜边AC交于点D,E为BC边的中点,连接DE.
已知:在Rt△ABC中,∠ABC=90°,以直角边AB为直径作⊙O,⊙O与斜边AC交于点D,E为BC边的中点,连接DE.(1)求证:DE是⊙O的切线;
(2)连接OE,若四边形AOED是平行四边形,求∠CAB的大小.
分析:(1)D点已经在圆周上,要证DE为切线,只需证明∠ODE=90°,而这一结论可根据三角形全等来证明,即△OBE≌△ODE,依据为边角边.
(2)在(1)的基础上,加上三角形中位线定理,以求出∠CAB=45°.
(2)在(1)的基础上,加上三角形中位线定理,以求出∠CAB=45°.
解答: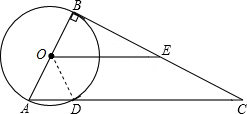 (1)证明:连接OD;
(1)证明:连接OD;
∵AO=BO,BE=CE,
∴OE∥AC.
∴∠BOE=∠A,∠EOD=∠ODA.
又∵OD=OA,
∴∠A=∠ODA,
∴∠EOD=∠EOB.
又∵OD=OB,OE=OE,
∴△DOE≌△BOE,
∴∠ODE=∠B=90°.
即DE是⊙O的切线.
(2)解:由(1)得,OE∥AC,且OE=
AC;
∵四边形AOED为平行四边形,
∴OE=AD=CD,
∴四边形OECD为平行四边形,
∴∠C=∠DOE.
又∵∠A=∠DOE且∠B=90°,
∴∠A=∠C=45°.
 (1)证明:连接OD;
(1)证明:连接OD;∵AO=BO,BE=CE,
∴OE∥AC.
∴∠BOE=∠A,∠EOD=∠ODA.
又∵OD=OA,
∴∠A=∠ODA,
∴∠EOD=∠EOB.
又∵OD=OB,OE=OE,
∴△DOE≌△BOE,
∴∠ODE=∠B=90°.
即DE是⊙O的切线.
(2)解:由(1)得,OE∥AC,且OE=
| 1 |
| 2 |
∵四边形AOED为平行四边形,
∴OE=AD=CD,
∴四边形OECD为平行四边形,
∴∠C=∠DOE.
又∵∠A=∠DOE且∠B=90°,
∴∠A=∠C=45°.
点评:此题考查了切线的判定和平行四边形的判定及性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
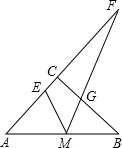 如图,已知:在Rt△ABC中,∠ACB=90°,AC=BC=4,M是边AB的中点,E、G分别是边AC、BC上的一点,∠EMG=45°,AC与MG的延长线相交于点F.
如图,已知:在Rt△ABC中,∠ACB=90°,AC=BC=4,M是边AB的中点,E、G分别是边AC、BC上的一点,∠EMG=45°,AC与MG的延长线相交于点F.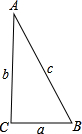 已知:在Rt△ABC中,∠C=90°,∠A=30°,b=
已知:在Rt△ABC中,∠C=90°,∠A=30°,b=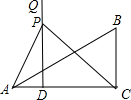 重合),过D作DQ⊥AC(DQ与AB在AC的同侧);点P从D点出发,在射线DQ上运动,连接PA、PC.
重合),过D作DQ⊥AC(DQ与AB在AC的同侧);点P从D点出发,在射线DQ上运动,连接PA、PC.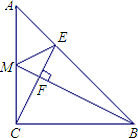 已知:在Rt△ABC中,∠C=90°,AC=BC,M是AC的中点,连接BM,CF⊥MB,F是垂足,延长CF交AB于点E.求证:∠AME=∠CMB.
已知:在Rt△ABC中,∠C=90°,AC=BC,M是AC的中点,连接BM,CF⊥MB,F是垂足,延长CF交AB于点E.求证:∠AME=∠CMB. 已知:在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.
已知:在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.