题目内容
【题目】如图,AB是⊙O的直径,BC是⊙O的弦,半径OD⊥BC,垂足为E,若BC= ![]() ,DE=3.
,DE=3.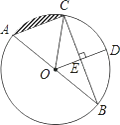
求:
(1)⊙O的半径;
(2)弦AC的长;
(3)阴影部分的面积.
【答案】
(1)解:∵半径OD⊥BC,∴CE=BE,∵BC= ![]() ,∴CE=
,∴CE= ![]() ,设OC=x,在直角三角形OCE中,OC2=CE2+OE2,∴x2=(
,设OC=x,在直角三角形OCE中,OC2=CE2+OE2,∴x2=( ![]() )2+(x﹣3)2,∴x=6,即半径OC=6;
)2+(x﹣3)2,∴x=6,即半径OC=6;
(2)解:∵AB为直径,∴∠ACB=90°,AB=12,又∵BC= ![]() ,∴AC2=AB2﹣BC2=36,∴AC=6
,∴AC2=AB2﹣BC2=36,∴AC=6
(3)解:∵OA=OC=AC=6,∴∠AOC=60°,∴S阴=S扇﹣S△OAC= ![]() ﹣
﹣ ![]()
= ![]()
【解析】(1)根据垂径定理和勾股定理求出⊙O的半径;(2)由AB为直径,得到圆周角∠ACB=90°,根据勾股定理求出弦AC的长;(3)根据S阴=S扇﹣S△OAC求出阴影部分的面积.
【考点精析】认真审题,首先需要了解垂径定理(垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧),还要掌握扇形面积计算公式(在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2))的相关知识才是答题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目