题目内容
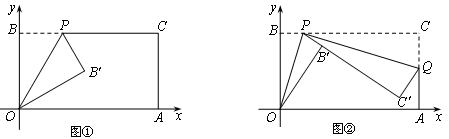
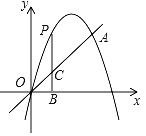
【题目】已知:如图,抛物线y=ax2+4x+c经过原点O(0,0)和点A (3,3),P为抛物线上的一个动点,过点P作x轴的垂线,垂足为B(m,0),并与直线OA交于点C.
(1)求抛物线的解析式;
(2)当点P在直线OA上方时,求线段PC的最大值.
【答案】(1)y=﹣x2+4x;(2)![]() .
.
【解析】
(1)把A与O坐标代入抛物线解析式求出a与c的值,即可求出解析式;
(2)根据题意表示出P与C的纵坐标,进而表示出线段PC的长,确定出最大值即可.
解:(1)把O(0,0),A(3,3)代入得:![]() ,
,
解得:![]() ,
,
则抛物线解析式为y=﹣x2+4x;
(2)设直线OA解析式为y=kx,
把A(3,3)代入得:k=1,即直线OA解析式为y=x,
∵PB⊥x轴,
∴P,C,B三点横坐标相等,
∵B(m,0),
∴把x=m代入y=x中得:y=m,即C(m,m),
把x=m代入y=﹣x2+4x中得:y=﹣m2+4m,即P(m,﹣m2+4m),
∵P在直线OA上方,
∴PC=﹣m2+4m﹣m=﹣m2+3m(0<m<3),
当m=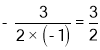 时,PC取得最大值,最大值为
时,PC取得最大值,最大值为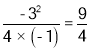 .
.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案【题目】某校举行汉字听写大赛,学习对参赛者获奖情况进行统计,根据比赛成绩列出统计表,并绘制了扇形统计图
(1)参加此次比赛的学生共______________人.
(2)![]()
(3)若从一等奖中随机抽取两名学生,参加市级汉字听写大赛,请用树状图或列表的方法,求出所选的两名学生正好为一男一女的概率.
等次 | 男生 | 女生 |
一等奖 | 3 | m |
二等奖 | 6 | 12 |
三等奖 | 8 | 9 |
鼓励奖 | 6 | n |

【题目】某学校为了解九年级男同学1000米跑步的成绩,随机抽取了部分男生进行测试,并将测试成绩分为A、B、C、D四个等级,绘制了不完整的成绩等级频数表和扇形统计图.
成绩等级 | 频数 |
A | 24 |
B | 10 |
C | b |
D | 2 |
合计 | a |
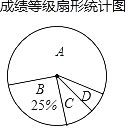
(1)表中a= ,b= ;
(2)扇形图中C的圆心角度数是 ;
(3)若该校共有九年级男生600人,请估计没有获得A等级的学生人数.