Question

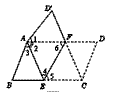
将平行四边形纸片ABCD按如图方式折叠，使点C与A重合，点D落到D′ 处，折痕为EF．

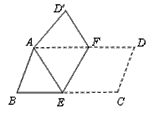（1）求证：△ABE≌△AD′F； （2）连接CF，判断四边形AECF是什么特殊四边形？证明你的结论．

Answer 1

解：（1） 由折叠可知：∠D=∠D′，CD=AD′，∠C=∠D′AE ∵四边形ABCD是平行四边形  ∴∠B=∠D，AB=CD，∠C=∠BAD ∴∠B=∠D′，AB=AD′ ∠D′AE=∠BAD，即∠1+∠2=∠2+∠3 ∴∠1=∠3  ∴△ABE ≌△A D′F （ASA）； （2）结论： 四边形AECF是菱形 理由：由折叠可知：AE=EC，∠4=∠5．  ∵四边形ABCD是平行四边形， ∴AD∥BC ∴∠5=∠6 ∴∠4=∠6 ∴AF=AE ∵AE=EC， ∴AF=EC 又∵AF∥EC， ∴四边形AECF是平行四边形 ∵AF=AE， ∴四边形AECF是菱形。