题目内容
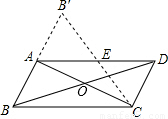
如图1，平行四边形纸片ABCD的面积为120，AD=20，AB=18．今沿两对角线将四边形ABCD剪成甲、乙、丙、丁四个三角形纸片．若将甲、丙合并（AD、CB重合）形成对称图形戊，如图2所示，则图形戊的两条对角线长度之和是
分析：由题意可得对角线EF⊥AD，且EF与平行四边形的高相等，进而利用面积与边的关系求出BC边的高即可．
解答：解：如图，则可得对角线EF⊥AD，且EF与平行四边形的高相等．
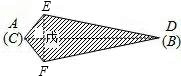
∵平行四边形纸片ABCD的面积为120，AD=20，
∴EF=
=6，
又BC=20，
∴对角线之和为20+6=26，
故应填：26．
∵平行四边形纸片ABCD的面积为120，AD=20，
∴EF=
| 120 |
| 20 |
又BC=20，
∴对角线之和为20+6=26，
故应填：26．
点评：本题主要考查平行四边形的性质以及图形的对称问题，应熟练掌握．
练习册系列答案
名校课堂系列答案
相关题目
22、如图，在平行四边形ABCD纸片中，AC⊥AB，AC与BD相交于O，将纸△ABC沿对角线AC翻转180°，得到△AB′C，问以A、C、D、B′为顶点的四边形是什么形状的四边形？证明你的结论．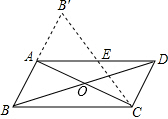
180°，得到△AB′C．
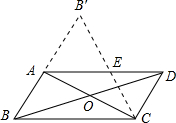如图，在平行四边形ABCD纸片中，AC⊥AB，AC与BD相交于O，将纸△ABC沿对角线AC翻转180°，得到△AB′C，
