Question

（2013•德惠市二模）如图，将平行四边形纸片ABCD沿对角线AC折叠，点D落在点E处，AE恰好过BC边中点，若AB=3，BC=6，则∠B的大小为（　　）

A．30°

B．45°

C．60°

D．90°

Answer 1

分析：AE与BC相交于F点，根据平行四边形的性质得AD∥BC，则∠1=∠3，再根据折叠性质得∠1=∠2，所以FC=FA，由于F为BC边中点，可得到AF=CF=BF=3，
而AB=3，于是可判断△ABF为等边三角形，然后根据等边三角形的性质即可得到∠B=60°．

解答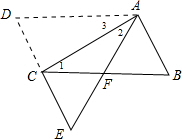：解：AE与BC相交于F点，如图，
∵四边形ABCD为平行四边形，
∴AD∥BC，
∴∠1=∠3，
∵平行四边形纸片ABCD沿对角线AC折叠，点D落在点E处，
∴∠2=∠3，
∴∠1=∠2，
∴FC=FA，
∵F为BC边中点，BC=6，
∴AF=CF=BF=

1

2

×6=3，
而AB=3，
∴△ABF为等边三角形，
∴∠B=60°．
故选C．

点评：本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了平时四边形的性质和等边三角形的判定与性质．