题目内容
已知关于x的一元二次方程mx 2-(3m+2)x+2m+2=0(m>0)
(1)求证:方程有两个不相等的实数根;
(2)设方程的两个实数根分别为x1、x2(x1<x2),若y是关于m的函数,且y=x2-2x1,求这个函数的解析式;
(3)在(2)的条件下,结合函数的图像回答:当自变量m的取值范围满足什么条件时,y≤2m.
(1)求证:方程有两个不相等的实数根;
(2)设方程的两个实数根分别为x1、x2(x1<x2),若y是关于m的函数,且y=x2-2x1,求这个函数的解析式;
(3)在(2)的条件下,结合函数的图像回答:当自变量m的取值范围满足什么条件时,y≤2m.
(1)证明见解析(2)y= (3)m≥1
(3)m≥1
 (3)m≥1
(3)m≥1(1)证明:∵a=m,b=-(3m+2),c=2m+2
∴ Δ=【-(3m+2)】2-4m(2m+2)
Δ=【-(3m+2)】2-4m(2m+2)
=9m2+12m+4-8m2-8m
=m2+4m+4
=(m+2)2
又∵m>0
∴Δ=(m+2)2>0
∴ 此方程有两个不相等的实数根
(2)先由公式法可求得x=1或x=
∵x1<x2
∴x1=1,x2 =
∴y=x2 -2x1= -2=
-2= (m>0)
(m>0)
(3)在同一直角坐标系中分别画出函数y= (m>0)和y1=2m的图像,由图像可得当m≥1时,y≤2m.图略.
(m>0)和y1=2m的图像,由图像可得当m≥1时,y≤2m.图略.
本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.本题也考查了不等式的解法,m>0是一个重要的条件.
∴
 Δ=【-(3m+2)】2-4m(2m+2)
Δ=【-(3m+2)】2-4m(2m+2)=9m2+12m+4-8m2-8m
=m2+4m+4
=(m+2)2
又∵m>0
∴Δ=(m+2)2>0
∴ 此方程有两个不相等的实数根
(2)先由公式法可求得x=1或x=

∵x1<x2
∴x1=1,x2 =

∴y=x2 -2x1=
 -2=
-2= (m>0)
(m>0)(3)在同一直角坐标系中分别画出函数y=
 (m>0)和y1=2m的图像,由图像可得当m≥1时,y≤2m.图略.
(m>0)和y1=2m的图像,由图像可得当m≥1时,y≤2m.图略.本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.本题也考查了不等式的解法,m>0是一个重要的条件.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 下降到9月份 的12600元/
下降到9月份 的12600元/ )
)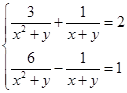 .
. 的一个根为2,则这个方程的另一个根是
的一个根为2,则这个方程的另一个根是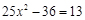
 的根为:( )
的根为:( )

 ,
,
 ,
,
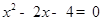 ;
;