题目内容
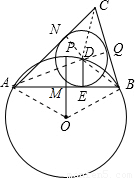
如图,⊙O的半径为1,点P是⊙O上一点,弦AB垂直平分线段OP,点D是弧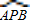 上任一点(与端点A、B不重合),DE⊥AB于点E,以点D为圆心、DE长为半径作⊙D,分别过点A、B作⊙D的切线,两条切线相交于点C.
上任一点(与端点A、B不重合),DE⊥AB于点E,以点D为圆心、DE长为半径作⊙D,分别过点A、B作⊙D的切线,两条切线相交于点C.①求∠ACB的度数为 ;
②记△ABC的面积为S,若
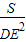 =4
=4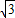 ,则⊙D的半径为 .
,则⊙D的半径为 .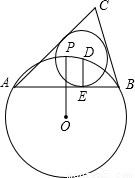
【答案】分析:①根据切线的判定定理得出AB与⊙D相切于E点,进而得出⊙D是△ABC的内切圆,根据OM= OP=0.5,得出∠MOB=60°,进而得出∠ACB的度数;
OP=0.5,得出∠MOB=60°,进而得出∠ACB的度数;
②根据S△ABC=S△ADC+S△ADB+S△BDC,得出△ABC的面积为S= (AB+AN+CN+BC)×DE,由切线长定理以及DE=DN=
(AB+AN+CN+BC)×DE,由切线长定理以及DE=DN= CD,
CD,
得出CN= DE,再利用已知求出⊙D的半径.
DE,再利用已知求出⊙D的半径.
解答:解:①连接AD,BD,OA,OB,
∵DE⊥AB于点E,点D为圆心、DE长为半径作⊙D,
∴AB与⊙D相切于E点,
又∵过点A、B作⊙D的切线,
∴⊙D是△ABC的内切圆,
∵⊙O的半径为1,
∴OP=1,
∵弦AB垂直平分线段OP,
∴OM= OP=0.5,
OP=0.5,
∴MO= OB,
OB,
∴∠MOB=60°,同理可得:∠AOB=120°,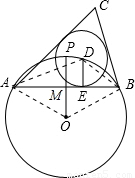
∴∠DAB+∠DBA= (∠CAB+∠CBA)=60°,
(∠CAB+∠CBA)=60°,
∴∠ACB的度数为60°,
故答案为:60°;
②∵OM= OP=0.5,
OP=0.5,
∴BM=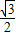 ,AB=
,AB=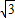 ,
,
∵AE=AN,BE=BQ,
∴△ABC的面积为S= (AB+AN+CN+BC)×DE=
(AB+AN+CN+BC)×DE= (2
(2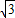 +2CN)×DE,
+2CN)×DE,
∵△ABC的面积为S,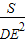 =4
=4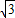 ,
,
∴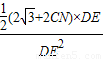 =4
=4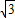 ,
,
∵DE=DN= CD,
CD,
∴CN=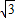 DE,
DE,
∴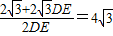 ,
,
解得:DE= ,
,
则⊙D的半径为: ,
,
故答案为: .
.
点评:此题主要考查了三角形内切圆性质与圆周角定理和垂径定理等知识,题目综合性较强,得出S△ABC=S△ADC+S△ADB+S△BDC是解决问题的关键.
 OP=0.5,得出∠MOB=60°,进而得出∠ACB的度数;
OP=0.5,得出∠MOB=60°,进而得出∠ACB的度数;②根据S△ABC=S△ADC+S△ADB+S△BDC,得出△ABC的面积为S=
 (AB+AN+CN+BC)×DE,由切线长定理以及DE=DN=
(AB+AN+CN+BC)×DE,由切线长定理以及DE=DN= CD,
CD,得出CN=
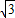 DE,再利用已知求出⊙D的半径.
DE,再利用已知求出⊙D的半径.解答:解:①连接AD,BD,OA,OB,
∵DE⊥AB于点E,点D为圆心、DE长为半径作⊙D,
∴AB与⊙D相切于E点,
又∵过点A、B作⊙D的切线,
∴⊙D是△ABC的内切圆,
∵⊙O的半径为1,
∴OP=1,
∵弦AB垂直平分线段OP,
∴OM=
 OP=0.5,
OP=0.5,∴MO=
 OB,
OB,∴∠MOB=60°,同理可得:∠AOB=120°,

∴∠DAB+∠DBA=
 (∠CAB+∠CBA)=60°,
(∠CAB+∠CBA)=60°,∴∠ACB的度数为60°,
故答案为:60°;
②∵OM=
 OP=0.5,
OP=0.5,∴BM=
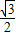 ,AB=
,AB=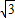 ,
,∵AE=AN,BE=BQ,
∴△ABC的面积为S=
 (AB+AN+CN+BC)×DE=
(AB+AN+CN+BC)×DE= (2
(2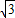 +2CN)×DE,
+2CN)×DE,∵△ABC的面积为S,
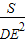 =4
=4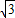 ,
,
∴
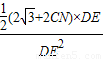 =4
=4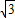 ,
,∵DE=DN=
 CD,
CD,∴CN=
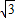 DE,
DE,∴
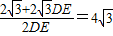 ,
,解得:DE=
 ,
,则⊙D的半径为:
 ,
,故答案为:
 .
.点评:此题主要考查了三角形内切圆性质与圆周角定理和垂径定理等知识,题目综合性较强,得出S△ABC=S△ADC+S△ADB+S△BDC是解决问题的关键.

练习册系列答案
相关题目
 如图,⊙O的半径为5,AB=5
如图,⊙O的半径为5,AB=5 如图,⊙O的半径为3,直径AB⊥弦CD,垂足为E,点F是BC的中点,那么EF2+OF2=
如图,⊙O的半径为3,直径AB⊥弦CD,垂足为E,点F是BC的中点,那么EF2+OF2= 如图,⊙O的半径为
如图,⊙O的半径为 如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的两侧,AB=24cm,CD=10cm,求AB和CD的距离.
如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的两侧,AB=24cm,CD=10cm,求AB和CD的距离. 如图,⊙O的半径为5,P是弦MN上的一点,且MP:PN=1:2.若PA=2,则MN的长为
如图,⊙O的半径为5,P是弦MN上的一点,且MP:PN=1:2.若PA=2,则MN的长为