题目内容
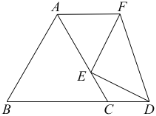
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 向终点
向终点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 运动,它们的速度均为每秒5个单位长度,点
运动,它们的速度均为每秒5个单位长度,点![]() 到达终点时,
到达终点时,![]() 、
、![]() 同时停止运动.当点
同时停止运动.当点![]() 不与点
不与点![]() 、
、![]() 重合时,过点
重合时,过点![]() 作
作![]() 于点
于点![]() ,连结
,连结![]() ,以
,以![]() 、
、![]() 为邻边作
为邻边作![]() .设
.设![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,运动时间为
,运动时间为![]() 秒.
秒.
(1)用含![]() 的代数式表示
的代数式表示![]() 的长为________;
的长为________;
(2)是否存在某一时刻![]() ,使四边形
,使四边形![]() 为矩形,若存在,求出
为矩形,若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)![]() 时,求
时,求![]() 与
与![]() 的函数关系式.
的函数关系式.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() ;(3)
;(3)![]() 与
与![]() 之间的函数关系式为
之间的函数关系式为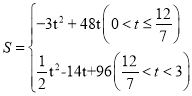 .
.
【解析】
(1)根据三角函数即可计算出PN的长度;
(2)当口POMN为矩形时,由PN⊥AB可得PQ//AB,再根据平行线分线段成比例定理可得![]() ,最后计算即可;
,最后计算即可;
(3)分![]() 在三角形内部时和
在三角形内部时和![]() 有部分在外边时,分别由三角函数可计算各图形中的高,最后运用三角形的面积公式解答即可.
有部分在外边时,分别由三角函数可计算各图形中的高,最后运用三角形的面积公式解答即可.
解:(1)∵在Rt△ABC中,C=90°,AC=20,BC=15.
∴AB=![]()
∴sin∠CAB=![]()
由题可知AP=5t.
则PN=AP·sin∠CAB=5t×![]() =3t.
=3t.
故答案为:![]() ;
;
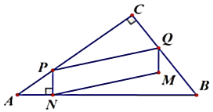
(2)当![]() 为矩形时,
为矩形时,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
由题意可知![]() ,
,![]() ,
,
∴![]() ,
,
解得;![]() ,
,
即当![]() 为矩形时
为矩形时![]() .
.
(3)
①如图所示.![]() 在三角形内部时.延长
在三角形内部时.延长![]() 交
交![]() 于
于![]() 点,
点,
由(1)题可知:![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,
![]() ,
,
![]() ,
,
∵![]() 在三角形内部时.有
在三角形内部时.有![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() .
.
∴当![]() 时,
时,![]() 与
与![]() 重叠部分图形为
重叠部分图形为![]() ,
,![]() 与
与![]() 之间的函数关系
之间的函数关系
式为![]() .
.
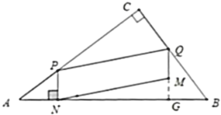
②如图所示.当![]() 时,
时,![]() 与
与![]() 重叠部分图形为梯形
重叠部分图形为梯形![]() ,
,
即:![]() ,
,
解得:![]() ,
,
![]() 与
与![]() 重叠部分图形为梯形
重叠部分图形为梯形![]() 的面积
的面积
![]()
当![]() ,
,![]() .
.
综上,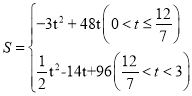

练习册系列答案
相关题目