题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,分别与AC,BC交于点E,F. 过点F作⊙O的切线交AB于点M.

(1)求证:MF⊥AB;
(2)若⊙O的直径是6,填空:
①连接OF,OM,当FM= 时,四边形OMBF是平行四边形;
②连接DE,DF,当AC= 时,四边形CEDF是正方形.
【答案】(1)证明见解析;(2)①(2)3;②![]() .
.
【解析】
(1)连接OF,则OF=OC,得出∠OCF=∠OFC,由CD是斜边AB上的中线得出CD=BD=![]() AB,则∠OCF=∠B,推出∠ONF=∠B,得出OF∥AB,又由OF⊥FM,得出AB⊥FM,即可得出结论;
AB,则∠OCF=∠B,推出∠ONF=∠B,得出OF∥AB,又由OF⊥FM,得出AB⊥FM,即可得出结论;
(2)①由四边形OMBF是平行四边形,可以得到MB=OF=3,且DB=DC=6,进一步得到DM=DB-MB=6-3=3,此时M是DB中点,进而得到FM为△BCD的中位线,得到FM∥CD,由FM⊥AB,得到此时CD⊥AB,此时四边形FODM为矩形,FM=OD=3即可.
②连接ED,当四边形CEDF为正方形时可以得出∠ECD=∠CDE=45°,进一步求出CE的长,由DA=DC,可以得到△DAC为等腰三角形,由“三线合一”得出AC=2CE即可求解.
(1)连接OF,
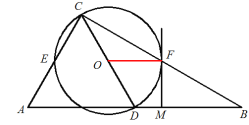
∵CD是直角△ABC斜边的中线,
∴CD=BD,
∴∠DCB=∠B,
∵OC=OF,
∴∠OCF=∠OFC,
∴∠OFC=∠B,
∴OF∥BD,
∵FM是圆O的切线,
∴∠OFM=90°,
∴∠FMB=90°,即FM⊥AB;
(2)①如下图所示,连接OF,OM:
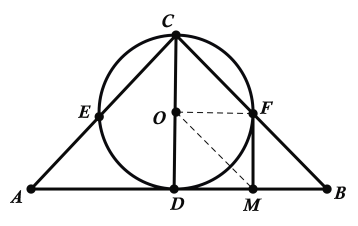
∵四边形OMBF为平行四边形
∴OF=MB=3
又CD=BD=6
∴DM=BD-MB=6-3=3,即M为DB的中点
∴FM为△CDB的中位线
∴FM∥CD
又FM⊥DB
∴CD⊥DB
且∠OFM=90°=∠FOD
∴四边形FODM为矩形
∴FM=OD=3
故答案为:3.
②连接DE和DF,如下图所示:
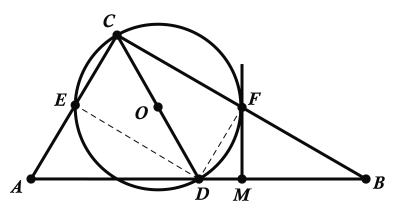
∵CD为圆O的直径,∴∠CED=90°,∠CFD=90°
且∠ACB=90°
∴四边形CEDF为矩形
当四边形CEDF为正方形时,有∠CED=∠CDE=45°
∴△CED为等腰直角三角形,其三边之比为:![]() ,且CD=6
,且CD=6
∴CE=![]() CD=
CD=![]()
又DC=DA
∴△ACD为等腰三角形
由等腰三角形的“三线合一”性质知:
AC=2CE=![]()
故答案为:![]()

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案