题目内容
【题目】如图,直线AB,CD,EF相交于点O,OG是∠AOF的平分线,∠BOD=35°,∠COE=18°,则∠COG的度数是________.
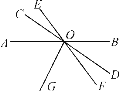
【答案】98.5°
【解析】
已知∠BOD、∠COE的度数,根据对顶角相等可求出∠AOC、∠DOF的度数,∠BOD已知,∠DOF已求出,则∠AOF的度数可求出,再根据OG 是∠AOF的平分线,进一步求出∠AOG,再根据∠COG=∠AOC+∠AOG,则∠COG的度数即可求得.
∵∠BOD=35°,
∴∠AOC=35°,
∵∠COE=18°,
∴∠DOF=18°,
∴∠BOF=∠BOD+∠DOF=35°+18°=53°,
∴∠AOF=180°-53°=127°,
∵OG平分∠AOF,
∴∠AOG=∠GOF=![]() ∠AOF=
∠AOF=![]() ×127°=63.5°,
×127°=63.5°,
∴∠COG=∠AOC+∠AOG=35°+63.5°=98.5°.
故答案为:98.5°

练习册系列答案
相关题目