题目内容
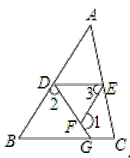
【题目】如图,在直线1上依次摆放着四个正方形和三个等腰直角三角形(阴影图形),已知三个等腰直角三角形的面积从左到右分别为1、2、3,四个正方形的面积从左到右依次是S1、S2、S3、S4,则S1+S2+S3+S4的值为( )

A. 4 B. 5 C. 6 D. 8
【答案】D
【解析】
将已知的等腰直角三角形翻折得到时故正方形如图所示,运用勾股定理可知,每两个相邻的正方形面积和都等于中间斜放的正方形面积,据此即可解答.
观察发现,
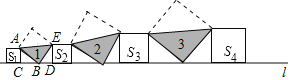
∵AB=BE,∠ACB=∠BDE=90°,
∴∠ABC+∠BAC=90°,∠ABC+∠EBD=90°,
∴∠BAC=∠EBD,
∴△ABC≌△BDE(AAS),
∴BC=ED,
∵AB2=AC2+BC2,
∴AB2=AC2+ED2=S1+S2,
即S1+S2=2,
同理S3+S4=6.
则S1+S2+S3+S4=2+6=8.
故选D.

练习册系列答案
相关题目
【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | ||
5≤x<6 | 10 | 20% |
6≤x<7 | 12% | |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |

(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.