题目内容
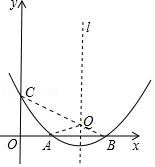
【题目】如图，抛物线y=ax2+bx+c（a≠0）的顶点坐标为（4，﹣ 
），且与y轴交于点C（0，2），与x轴交于A，B两点（点A在点B的左边）
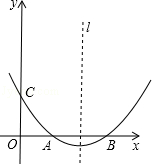
（1）求抛物线的解析式及A，B两点的坐标；
（2）若（1）中抛物线的对称轴上有点P，使△ABP的面积等于△ABC的面积的2倍，求出点P的坐标；
（3）在（1）中抛物线的对称轴l上是否存在一点Q，使AQ+CQ的值最小？若存在，求AQ+CQ的最小值；若不存在，请说明理由．
【答案】
（1）
解：抛物线的顶点坐标为（4，﹣ 
），可以假设抛物线为y=a（x﹣4）2﹣ 把点（0，2）代入得到a= 
，
∴抛物线的解析式为y= （x﹣4）2﹣ ．
令y=0得到 （x﹣4）2﹣ =0，解得x=2或6，
∴A（2，0），B（6，0）
（2）
解：设P（4，m），
由题意： 
4|m|=2× ×4×2，解得m=±4，
∴点P坐标（4，4）或（4，﹣4）
（3）
解：存在．理由如下：
∵A、B关于对称轴对称，连接CB交对称轴于Q，连接QA，此时QA+QC最短（两点之间线段最短），
∴QA+QC的最小值=QA+QC=QB+QC=BC= 
= 
．
【解析】（1）因为抛物线的顶点坐标为（4，﹣ ），所以可以假设抛物线为y=a（x﹣4）2﹣ 把点（0，2）代入得到a= ，令y=0，解方程即可求出A、B两点坐标．（2）设P（4，m），由题意可得 4|m|=2× ×4×2，解方程即可．（3）存在．因为A、B关于对称轴对称，连接CB交对称轴于Q，连接QA，此时QA+QC最短（两点之间线段最短），
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案，需要熟知二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
