题目内容
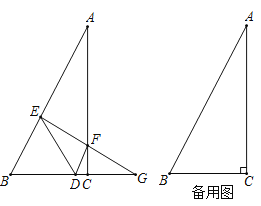
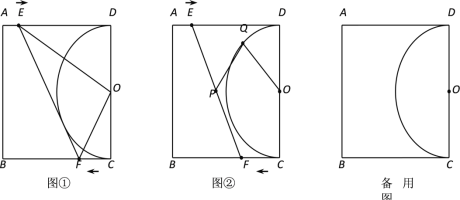
【题目】在正方形ABCD中,有一直径为CD的半圆,圆心为点O,CD=2,现有两点E、F,分别从点A、点C同时出发,点E沿线段AD以每秒1个单位长度的速度向点D运动,点F沿线段CB以每秒2个单位长度的速度向点B运动,当点F运动到点B时,点E也随之停止运动.设点E离开点A的时间为t(s),回答下列问题:
(1)如图①,根据下列条件,分别求出t的值.
①EF与半圆相切;
②△EOF是等腰三角形.
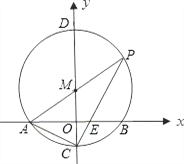
(2)如图②,点P是EF的中点,Q是半圆上一点,请直接写出PQ+OQ的最小值与最大值.
【答案】(1)①当EF与半圆相切时,t的值为1-![]() ;②当△EOF是等腰三角形时,t的值为
;②当△EOF是等腰三角形时,t的值为![]() 或1;(2)1、1+
或1;(2)1、1+![]() .
.
【解析】
(1)①如图,设EF与半圆相切于点G,由切线长定理可知ED=EG,FC=FG,在Rt△EHF中,利用勾股定理列出方程即可解决问题;
②分三种情形讨论,分别列出方程求解即可;
(2)①当点P在半圆上时,PQ的最小值为0,此时PQ+OQ的最小值为1.②当点F运动到B时,点P与点O之间的结论最大,当Q与D重合时,PQ+OQ的值最大;
(1)①设EF与半圆相切于点G,
过点E作EH⊥BC,垂足为点H.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=2,∠A=∠B=∠ADC=∠BCD=90°,
∴OD⊥AD,且AD经过半径OD的外端点D,
∴AD与半圆相切于点D,
同理可证:BC与半圆相切于点C,
∴ED=EG=2-t,CF=FG=2t,
∴EF=2+t,
∵EH⊥BC,垂足为点H,∴∠BHE=90°,
∵∠A=∠B=90°,∴四边形ABHE是矩形,
∴EH=AB=2,BH=AE=t,
∴HF=2-3t,
在△EHF中,∠EHF=90°,
∴EH2+HF2=EF2,
∴22+(2-3t)2=(2+t)2,
解这个方程,得t1=1-![]() <1,t2=1+
<1,t2=1+![]() >1(不合题意,舍去),
>1(不合题意,舍去),
∴当EF与半圆相切时,t的值为1-![]() .
.
②解:在△EDO中,∵∠EDO=90°,∴OE2=t2-4t+5,
同理可证:OF2=1+4t2, EF2=9t2-12t+8,
第一种情况:当OE=OF时,则OE2=OF2,
∴t2-4t+5=1+4t2,
解这个方程,得t1=![]() <1,t2=-2<0(不合题意,舍去),
<1,t2=-2<0(不合题意,舍去),
第二种情况:当OE=EF时,则OE2=EF2,
∴t2-4t+5=9t2-12t+8,此方程无解,
第三种情况:当OF=EF时,则OF2=EF2,
∴1+4t2=9t2-12t+8,
解这个方程,得t1=1,t2=1.4>1(不合题意,舍去),
综上所述:当△EOF是等腰三角形时,t的值为![]() 或1.
或1.
(3)
由题意可知,点P在边CD的垂直平分线上,当运动开始的时候点P在圆周上,随着运动点P向做运动直到停止
当P在圆上时,取P、Q为同一点,PQ+OQ最小为1,
当点F运动到B时,点P与点O之间的结论最大,当Q与D重合时,PQ+OQ的值最大
=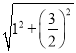 +1=1+
+1=1+![]()

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案