题目内容
【题目】如图,点E是等边△ABC内一点,且EA=EB,△ABC外一点D满足BD=AC,且BE平分∠DBC,则∠D=.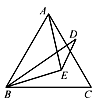
【答案】30°
【解析】(1)连接CE, 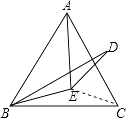
∵△ABC是等边三角形,
∴AC=BC,
在△BCE与△ACE中, 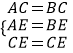
∴△BCE≌△ACE(SSS)
∴∠BCE=∠ACE=30°
∵BE平分∠DBC,
∴∠DBE=∠CBE,
在△BDE与△BCE中, 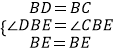
∴△BDE≌△BCE(SAS),
∴∠BDE=∠BCE=30°.
【考点精析】解答此题的关键在于理解角的平分线的相关知识,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线,以及对等边三角形的性质的理解,了解等边三角形的三个角都相等并且每个角都是60°.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目


